
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 6.3, Problem 39E
The center of a
(HINT: use similar
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
Elementary Geometry For College Students, 7e
Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - Given: AOOBandOCbisectsACBinO Find: a mAB b mACB c...Ch. 6.1 - Given: ST=12(SR)inQSRisadiameter Find: a mST b mTR...
Ch. 6.1 - Given: QinwhichmAB:mBC:mCA=2:3:4 Find: a mAB b mBC...Ch. 6.1 - Given: mDOE=76and mEOG=82inO EFisadiameter Find: a...Ch. 6.1 - Given: OwithABACand mBOC=72 Find: a mBC b mAB c mA...Ch. 6.1 - In O not shown, OA is a radius, AB is a diameter,...Ch. 6.1 - Given: In O,OCABand OC=6 Find: a AB b BC Exercise...Ch. 6.1 - Prob. 16ECh. 6.1 - Given: Concentric circles with center Q...Ch. 6.1 - AB is the common chord of O and Q. If AB=12 and...Ch. 6.1 - Circles O and Q have the common chord AB. If AB=6,...Ch. 6.1 - Suppose that a circle is divided into three...Ch. 6.1 - Suppose that a circle is divided by points A,B,C,...Ch. 6.1 - Prob. 22ECh. 6.1 - Prob. 23ECh. 6.1 - Prob. 24ECh. 6.1 - Prob. 25ECh. 6.1 - Five points are equally spaced on a circle. A...Ch. 6.1 - A ceiling fan has equally spaced blades. What is...Ch. 6.1 - A wheel has equally spaced lug bolts. What is the...Ch. 6.1 - An amusement park ride the Octopus has eight...Ch. 6.1 - In Exercises 30 and 31, complete each proof....Ch. 6.1 - Prob. 31ECh. 6.1 - In Exercises 32 to 37, write a paragraph proof....Ch. 6.1 - Prob. 33ECh. 6.1 - Prob. 34ECh. 6.1 - Prob. 35ECh. 6.1 - Prob. 36ECh. 6.1 - In Exercises 32 to 37, write a paragraph proof. If...Ch. 6.1 - If MNPQin O, explain why MNPQ is an isosceles...Ch. 6.1 - If STTV, explain why STV is an isosceles triangle.Ch. 6.1 - Prob. 40ECh. 6.1 - In O,OY=5 and XZ=6. If XWWY, find WZ.Ch. 6.2 - Given: mAB=92mDA=114mBC=138 Find:...Ch. 6.2 - Given: mDC=30 and mDABC is trisected at points A...Ch. 6.2 - Given: Circle O with diameter RS, tangent SW,...Ch. 6.2 - Prob. 4ECh. 6.2 - Prob. 5ECh. 6.2 - Is it possible for a a rectangle inscribed in a...Ch. 6.2 - Given: In Q, PR contains Q, MR is a tangent,...Ch. 6.2 - Given: AB and AC are tangent to O, mBC=126 Find:...Ch. 6.2 - Given: Tangent ABand AC to O mACB=68 Find:...Ch. 6.2 - Given: m1=72,mDC=34 Find: a)mABb)m2Ch. 6.2 - Given: m2=36mAB=4mDC Find: a)mABb)m1Ch. 6.2 - Given: m3=42 Find: a)mRTb)mRST Exercises 12,13Ch. 6.2 - Given: RSSTRT Find: a)mRTb)mRSTc)m3 Exercises...Ch. 6.2 - Given: m1=63mRS=3x+6mVT=x Find: mRS Exercises 14,...Ch. 6.2 - Given: m2=124mTV=x+1mSR=3(x+1) Find: mTV Exercises...Ch. 6.2 - Given: m1=71m2=33 Find: mCE and mBD Exercises 16,...Ch. 6.2 - Given: m1=62m2=26 Find: mCE and mBD Exercises 16,...Ch. 6.2 - aHow are R and T related? bFind mR if mT=112....Ch. 6.2 - Prob. 19ECh. 6.2 - A quadrilateral RSTV is circumscribed about a...Ch. 6.2 - In Exercises 21 and 22, complete each proof....Ch. 6.2 - In Exercises 21 and 22, complete each proof....Ch. 6.2 - Prob. 23ECh. 6.2 - Prob. 24ECh. 6.2 - Prob. 25ECh. 6.2 - Prob. 26ECh. 6.2 - An airplane reaches an altitude of 3mi above the...Ch. 6.2 - From the veranda of a beachfront hotel, Manny is...Ch. 6.2 - For the five-pointed star a regular pentagram...Ch. 6.2 - For the six-pointed star a regular hexagram...Ch. 6.2 - A satellite dish in the shape of a regular...Ch. 6.2 - In the figure shown, RSTWVT by the reason AA. Name...Ch. 6.2 - In the figure shown, RXVWXS by the reason AA. Name...Ch. 6.2 - On a fitting for a hex wrench, the distance from...Ch. 6.2 - Given: AB is a diameter of M is the midpoint of...Ch. 6.2 - A surveyor sees a circular planetarium through an...Ch. 6.2 - The larger circle is inscribed in a square with...Ch. 6.2 - In R,QS=2(PT). Also, mP=23. Find mVRS.Ch. 6.2 - Prob. 39ECh. 6.2 - Prob. 40ECh. 6.2 - Prob. 41ECh. 6.2 - In Exercises 39 to 47, provide a paragraph proof....Ch. 6.2 - Prob. 43ECh. 6.2 - Prob. 44ECh. 6.2 - Prob. 45ECh. 6.2 - Prob. 46ECh. 6.2 - Prob. 47ECh. 6.2 - Given concentric circles with center O, ABC is...Ch. 6.2 - Prob. 49ECh. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Sketch two circles that have: a No common tangents...Ch. 6.3 - Two congruent intersecting circles B and D not...Ch. 6.3 - Prob. 7ECh. 6.3 - Prob. 8ECh. 6.3 - Prob. 9ECh. 6.3 - Prob. 10ECh. 6.3 - Prob. 11ECh. 6.3 - Prob. 12ECh. 6.3 - Prob. 13ECh. 6.3 - Prob. 14ECh. 6.3 - Prob. 15ECh. 6.3 - Prob. 16ECh. 6.3 - For Exercises 17 to 20. See Theorem 6.3.6. Given:...Ch. 6.3 - For Exercises 17 to 2, See Theorem 6.3.6. Given:...Ch. 6.3 - Prob. 19ECh. 6.3 - For Exercises 17 to 2, See Theorem 6.3.6. Given:...Ch. 6.3 - Prob. 21ECh. 6.3 - In the figure for Exercises 21 to 24,RS is tangent...Ch. 6.3 - In the figure for Exercises 21 to 24,RS is tangent...Ch. 6.3 - Prob. 24ECh. 6.3 - For the two circles in figures a, b, and c, find...Ch. 6.3 - For the two circles in figures a, b, and c, find...Ch. 6.3 - In Exercises 27 to 30, provide a paragraph proof....Ch. 6.3 - Prob. 28ECh. 6.3 - In Exercises 27 to 30, provide a paragraph proof....Ch. 6.3 - Prob. 30ECh. 6.3 - Does it follow from Exercise 30 that ADE is also...Ch. 6.3 - Prob. 32ECh. 6.3 - The cylindrical brush on a vacuum cleaner is...Ch. 6.3 - Prob. 34ECh. 6.3 - Given: Tangents AB,BC,andACtoO at points M, N, and...Ch. 6.3 - Given: Q is inscribed in isosceles right RST. The...Ch. 6.3 - Given: AB is an external tangent to O and Q at...Ch. 6.3 - Prob. 38ECh. 6.3 - The center of a circle of radius 2 in. is at a...Ch. 6.3 - Circles O, P, and Q are tangent as shown at points...Ch. 6.3 - Prob. 41ECh. 6.3 - Prob. 42ECh. 6.3 - Prob. 43ECh. 6.3 - If the larger gear has 30 teeth and smaller gear...Ch. 6.3 - Prob. 45ECh. 6.3 - In Exercises 46 to 49, prove the stated theorem....Ch. 6.3 - Prob. 47ECh. 6.3 - Prob. 48ECh. 6.3 - Prob. 49ECh. 6.3 - Prob. 50ECh. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - Prob. 2ECh. 6.4 - Prob. 3ECh. 6.4 - Prob. 4ECh. 6.4 - Prob. 5ECh. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - Prob. 8ECh. 6.4 - Prob. 9ECh. 6.4 - Prob. 10ECh. 6.4 - X, Y, and Z are on circle O such that mXY=120,...Ch. 6.4 - Prob. 12ECh. 6.4 - Construct the two tangent segments to circle P not...Ch. 6.4 - Construct the two tangent segments to circle R not...Ch. 6.4 - Point V is in the exterior of circle Q not shown...Ch. 6.4 - Prob. 16ECh. 6.4 - Prob. 17ECh. 6.4 - Prob. 18ECh. 6.4 - Prob. 19ECh. 6.4 - a If mRSmTV, write an inequality that compares m1...Ch. 6.4 - a If MNPQ, write an inequality that compares the...Ch. 6.4 - Prob. 22ECh. 6.4 - Quadrilateral ABCD is inscribed in circle P not...Ch. 6.4 - Quadrilateral RSTV is inscribed in circle Q not...Ch. 6.4 - In circle O, points A, B, and C are on the circle...Ch. 6.4 - Prob. 26ECh. 6.4 - Prob. 27ECh. 6.4 - Triangle ABC is inscribed in circle O; AB=5, BC=6,...Ch. 6.4 - Given circle O with mBC=120, and mAC=130. a Which...Ch. 6.4 - Given that mAC:mBC:mAB=4:3:2 in circle O: a Which...Ch. 6.4 - Prob. 31ECh. 6.4 - Circle O has a diameter of length 20cm. Chord AB...Ch. 6.4 - Prob. 33ECh. 6.4 - A tangent ET is constructed to circle Q from...Ch. 6.4 - Prob. 35ECh. 6.4 - Prob. 36ECh. 6.4 - Prob. 37ECh. 6.4 - Prove: In a circle containing two unequal chords,...Ch. 6.4 - In O, chord AB chord CD. Radius OE is...Ch. 6.4 - In P, whose radius has length 8in., mAB=mBC=60....Ch. 6.4 - Prob. 41ECh. 6.CR - The length of the radius of a circle is 15 mm. The...Ch. 6.CR - Find the length of a chord that is 8 cm from the...Ch. 6.CR - Two circles intersect and have a common chord 10...Ch. 6.CR - Two circles intersect and have a common chord 12...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - Prob. 6CRCh. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - Prob. 9CRCh. 6.CR - Prob. 10CRCh. 6.CR - Given:Owithtangentlandm1=46 Find:m2, m3,m4,m5Ch. 6.CR - Given:Owithtangentlandm5=40 Find:m1,m2, m3,m4,Ch. 6.CR - Two circles are concentric. A chord of the larger...Ch. 6.CR - Two parallel chords of a circle each have length...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - Prob. 20CRCh. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - Given that CF is a tangent to the circle shown:...Ch. 6.CR - Given that CF is a tangent to the circle shown:...Ch. 6.CR - Given:DF-AC-inO OE=5x+4 OB=2x+19 Find:OECh. 6.CR - Given:OE-OB-inO DF=xx-2 AC=x+28 Find:DEandACCh. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - Given:OwithdiameterAC-andtangentDE...Ch. 6.CR - A square is inscribed in a circle with a radius of...Ch. 6.CR - A 30-60-90 triangle is inscribed in a circle with...Ch. 6.CR - A circle is inscribed in the right triangle. The...Ch. 6.CR - Given:OisinscribedinABC AB=9,BC=13,AC=10...Ch. 6.CR - In Q with ABQ and CDQ, mABmCD. Also, QPABandQRCD....Ch. 6.CT - a If mAB=88, then mACB=____________. b If mAB=92...Ch. 6.CT - a If mBC=69, then mBOC=_____________. b If mBC=64,...Ch. 6.CT - a If mBAC=24, then mBC=_____________. b If ABAC,...Ch. 6.CT - Complete each theorem: a An angle inscribed in a...Ch. 6.CT - Given that mAB=106 and mDC=32, find: a m1 b m2Ch. 6.CT - Given the tangents with mRT=146, find : a mRST b...Ch. 6.CT - Given the tangents with m3=46, find: a mRST b mRTCh. 6.CT - aBecause point Q is their common center, these...Ch. 6.CT - In O with diameter AC, OC=5 and AB=6. If M is the...Ch. 6.CT - For the circles described and shown, how many...Ch. 6.CT - aIf HP=4, PJ=5, and PM=2, find LP. bIf HP=x+1,...Ch. 6.CT - In the figure, TV is a tangent and TVWTXV. Find TV...Ch. 6.CT - Construct the tangent line to P at point X.Ch. 6.CT - aIf mABmCD, write an inequality that compares...Ch. 6.CT - In P not shown, the length of radius PA is 5....Ch. 6.CT - Provide the missing statements and reasons in the...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
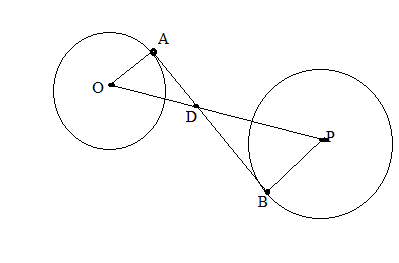
- The center of a circle of radius 2 inches is at a distance of 10 inches from the center of a circle of radius length 3 inches. To the nearest tenth of an inch, what is the approximate length of a common internal tangent? Use the hint provided in Exercise 38. HINT: use similar triangles to find OD and DP. Then apply the Pythagorean Theorem twice.arrow_forwardThe center of a circle of radius 3 inches is at a distance of 20 inches from the center of a circle of radius 9 inches. What is the exact length of common internal tangent AB? HINT: Use similar triangles to find OD and DP. Then apply the Pythagorean Theorem twice.arrow_forwardThe larger circle is inscribed in a square with sides of length 4cm. The smaller circle is tangent to the larger circle and to two sides of the square, as shown. Find the length of the radius of the smaller circle.arrow_forward
- Given concentric circles with center O, ABC is inscribed in the larger circle, as shown. If BC is tangent to the smaller circle at point T and AB=8, find the length of the radius of the smaller circle.arrow_forwardFor compactness, the drop-down wheels of a stretcher or gurney are folded under it as shown. In order for the boards upper surface to be parallel to the ground when the wheels are dropped, what relationship must exist between AB and CD?arrow_forwardIn order to make a conical duct, a circular sheet of metal is to be cut in the shape of a sector of a circle. If the radius of the sector is 28.5 in. and the arc length of the of the sector is 26.4 in., what are the central angle, , and area of the sector?arrow_forward
- A hot-air balloon is held in place by the ground crew at a point that is 21 ft from a point directly beneath the basket of the balloon. If the rope is of length 29 ft, how far above ground level is the basket?arrow_forwardGiven that the length of each side of a rhombus is 8 cm and that an interior angle measures 60. Find the area of the inscribed circle.arrow_forwardIn O with diameter AC, OC=5 and AB=6. If M is the midpoint of BC, find AM.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Finding the length of an arc; Author: Maths Genie;https://www.youtube.com/watch?v=fWGPf5peCc8;License: Standard YouTube License, CC-BY
Circles, Angle Measures, Arcs, Central & Inscribed Angles, Tangents, Secants & Chords - Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=nd46bA9DKE0;License: Standard Youtube License