Determine the smallest cross-sectional area A required for the members of the truss shown in Figure 1, so that the horizontal deflection at joint D does not exceed 10 mm. Use the virtual work method. 50 kN 50 kN 100 kN 4 m 3 m EA = constant E = 70 GPa
Determine the smallest cross-sectional area A required for the members of the truss shown in Figure 1, so that the horizontal deflection at joint D does not exceed 10 mm. Use the virtual work method. 50 kN 50 kN 100 kN 4 m 3 m EA = constant E = 70 GPa
Chapter6: Deflections Of Beams: Geometric Methods
Section: Chapter Questions
Problem 1P
Related questions
Question
determine the smallest cross-sectional area A required for the members of the truss shown in figure1, so that the horizontal deflection at joint D does not exceed 10 mm. use the virtual work method
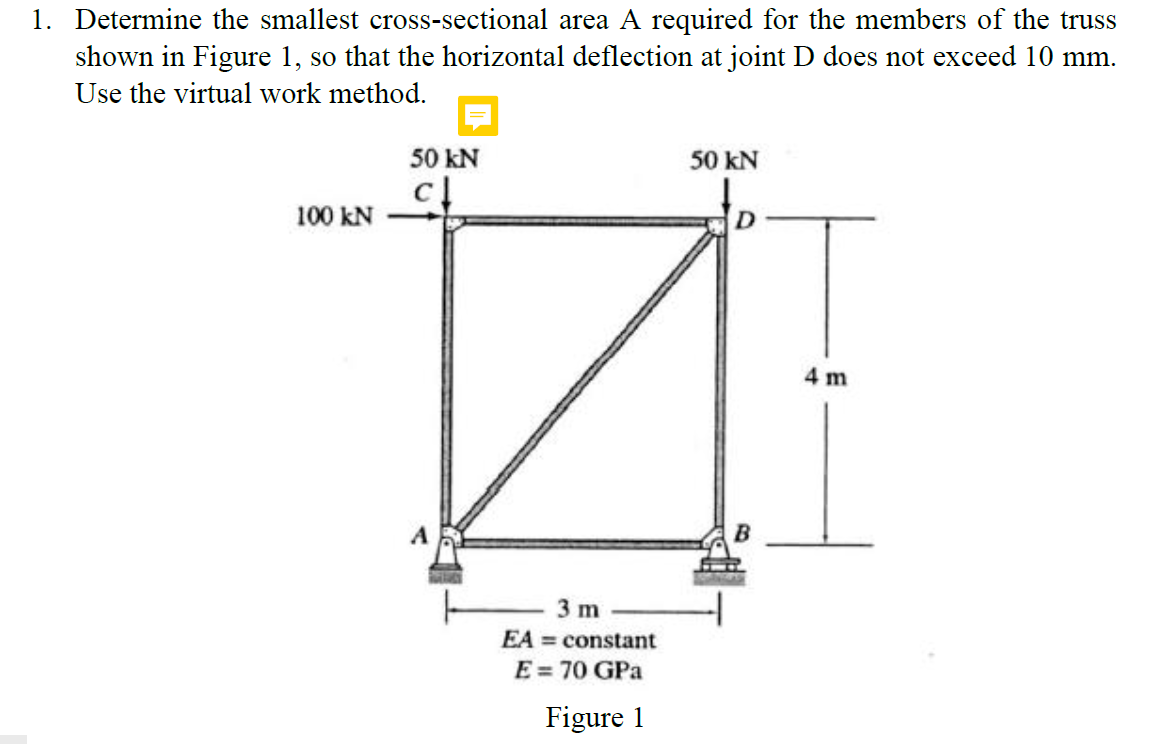
Transcribed Image Text:Determine the smallest cross-sectional area A required for the members of the truss
shown in Figure 1, so that the horizontal deflection at joint D does not exceed 10 mm.
Use the virtual work method.
50 kN
50 kN
100 kN
4 m
3 m
EA = constant
E = 70 GPa
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 7 steps with 11 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

