University Physics Volume 3
17th Edition
ISBN:9781938168185
Author:William Moebs, Jeff Sanny
Publisher:William Moebs, Jeff Sanny
Chapter9: Condensed Matter Physics
Section: Chapter Questions
Problem 98AP: Find the average energy of an electron in a Zn wire.
Related questions
Question
A snowboarder drops from rest into a halfpipe of radius
R and slides down its frictionless surface to the bottom (Fig.
P7.28). Show that (a) the snowboarder’s speed at the bottom
of the halfpipe is v =√2gR (Hint: Use conservation of energy), (b) the snowboarder’s centripetal acceleration at
the bottom is ac = 2g, and (c) the normal force on the snowboarder
at the bottom of the halfpipe has magnitude 3mg
(Hint : Use Newton’s second law of motion).
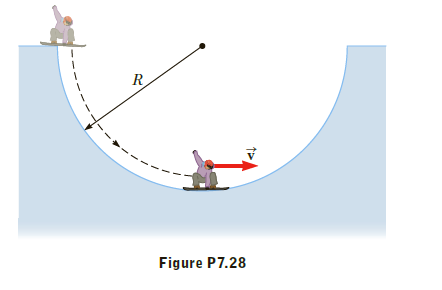
Transcribed Image Text:R
Figure P7.28
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Recommended textbooks for you

University Physics Volume 3
Physics
ISBN:
9781938168185
Author:
William Moebs, Jeff Sanny
Publisher:
OpenStax


Glencoe Physics: Principles and Problems, Student…
Physics
ISBN:
9780078807213
Author:
Paul W. Zitzewitz
Publisher:
Glencoe/McGraw-Hill

University Physics Volume 3
Physics
ISBN:
9781938168185
Author:
William Moebs, Jeff Sanny
Publisher:
OpenStax


Glencoe Physics: Principles and Problems, Student…
Physics
ISBN:
9780078807213
Author:
Paul W. Zitzewitz
Publisher:
Glencoe/McGraw-Hill