
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 7, Problem 69AP
A 4.0-kg object is attached to a vertical rod by two strings as shown in Figure P7.69. The object rotates in a horizontal circle at constant speed 6.00 m/s. Find the tension in (a) the upper string and (b) the lower string.
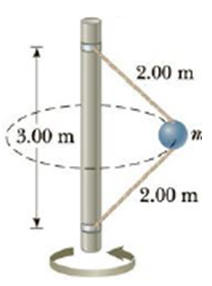
Figure P7.69
Expert Solution & Answer
Trending nowThis is a popular solution!

Students have asked these similar questions
A model airplane of mass 0.750 kg flies with a speed of 35 m/s in a horizontal circle at the end of a 60.0 m control wire as shown (See P7.62a) The forces exerted on the airplane are shown (See P7.62b), the tension in the control wire, angle = 20.0 degrees inward from the vertical. Compute the tension in the wire, assuming the wire makes a constant angle of 20.0 degrees.
A rocket powered car is set inside a circular track and ignited. Pressure sensors on the wall of the track measure the centripetal acceleration of the car as a function of time to be
?c(?)=(4 m/s6)?4+(28 m/s4)?2+(49 m/s2)
If the radius of the track is 3.28 m, what is the tangential acceleration of the rocket car at ?=5.51 s?
23. A highway has a flat section with a tight level curve of radius 40 m. If the coefficient of static friction between tires and pavement surface is 0.45, what is the maximum speed v at which the car of mass m can negotiate the curve safely – in other words, without the tires slipping? (Hint: the friction force between tires and pavement = coefficient of static friction times normal force) *use g=9.8
a. 18 m/s
b. 23 m/s
c. 15 m/s
d. 13 m/s
e. 10 m/s
Chapter 7 Solutions
College Physics
Ch. 7.1 - A rigid body is rotating counterclockwise about a...Ch. 7.1 - Suppose the change in angular position for each of...Ch. 7.2 - Consider again the pairs of angular positions for...Ch. 7.3 - Andrea and Chuck are riding on a merry-go-round....Ch. 7.3 - When the merry-go-round of Quick Quiz 7.4 is...Ch. 7.3 - A racetrack is constructed such that two arcs of...Ch. 7.3 - An object moves in a circular path with constant...Ch. 7.5 - A ball is falling toward the ground. Which of the...Ch. 7.5 - A planet has two moons with identical mass. Moon 1...Ch. 7.5 - Suppose an asteroid has a semimajor axis of 4 AU....
Ch. 7 - A disk rotates about an axis through its center....Ch. 7 - Suppose an alien civilization has a space station...Ch. 7 - If a cars wheels are replaced with wheels of...Ch. 7 - Objects moving along a circular path have a...Ch. 7 - A pendulum consists of a small object called a bob...Ch. 7 - Because of Earths rotation about its axis, you...Ch. 7 - It has been suggested that rotating cylinders...Ch. 7 - Describe the path of a moving object in the event...Ch. 7 - A pail of water can be whirled in a vertical...Ch. 7 - A car of mass m follows a truck of mass 2m around...Ch. 7 - Is it possible for a car to move in a circular...Ch. 7 - A child is practicing for a BMX race. His speed...Ch. 7 - An object executes circular motion with constant...Ch. 7 - Convert (a) 47.0 to radians, (b) 12.0 rad to...Ch. 7 - A bicycle tire is spinning clockwise at 2.50...Ch. 7 - The tires on a new compact car have a diameter of...Ch. 7 - A potters wheel moves uniformly from rest to an...Ch. 7 - A dentists drill starts from rest. After 3.20 s of...Ch. 7 - A centrifuge in a medical laboratory rotates at an...Ch. 7 - A bicyclist starting at rest produces a constant...Ch. 7 - A bicycle is turned upside down while its owner...Ch. 7 - The diameters of the main rotor and tail rotor of...Ch. 7 - The tub of a washer goes into its spin-dry cycle,...Ch. 7 - A car initially traveling at 29.0 m/s undergoes a...Ch. 7 - A 45.0-cm diameter disk rotates with a constant...Ch. 7 - A rotating wheel requires 3.00 s to rotate 37.0...Ch. 7 - An electric motor rotating a workshop grinding...Ch. 7 - A car initially traveling eastward turns north by...Ch. 7 - It has been suggested that rotating cylinders...Ch. 7 - (a) What is the tangential acceleration of a bug...Ch. 7 - An adventurous archeologist (m = 85.0 kg) tries to...Ch. 7 - One end of a cord is fixed and a small 0.500-kg...Ch. 7 - Human centrifuges are used to train military...Ch. 7 - A 55.0-kg ice skater is moving at 4.00 m/s when...Ch. 7 - A 40.0-kg child swings in a swing supported by two...Ch. 7 - A certain light truck can go around a flat curve...Ch. 7 - A sample of blood is placed in a centrifuge of...Ch. 7 - A 50.0-kg child stands at the rim of a...Ch. 7 - A space habitat for a long space voyage consists...Ch. 7 - An air puck of mass m1 = 0.25 kg is tied to a...Ch. 7 - A snowboarder drops from rest into a halfpipe of...Ch. 7 - A woman places her briefcase on the backseat of...Ch. 7 - A pail of water is rotated in a vertical circle of...Ch. 7 - A 40.0-kg child takes a ride on a Ferris wheel...Ch. 7 - Prob. 32PCh. 7 - (a) Find the magnitude of the gravitational force...Ch. 7 - The International Space Station has a mass of 4.19...Ch. 7 - A coordinate system (in meters) is constructed on...Ch. 7 - Prob. 36PCh. 7 - Objects with masses of 200. kg and 500. kg are...Ch. 7 - Use the data of Table 7.3 to find the point...Ch. 7 - Prob. 39PCh. 7 - Two objects attract each other with a...Ch. 7 - Prob. 41PCh. 7 - Prob. 42PCh. 7 - A satellite of Mars, called Phoebus, has an...Ch. 7 - Prob. 44PCh. 7 - A comet has a period of 76.3 years and moves in an...Ch. 7 - Additional Problems A synchronous satellite. which...Ch. 7 - (a) One of the moons of Jupiter, named Io, has an...Ch. 7 - Neutron stars are extremely dense objects that are...Ch. 7 - One method of pitching a softball is called the...Ch. 7 - A digital audio compact disc (CD) carries data...Ch. 7 - An athlete swings a 5.00-kg ball horizontally on...Ch. 7 - The dung beetle is known as one of the strongest...Ch. 7 - Prob. 53APCh. 7 - A 0.400-kg pendulum bob passes through the lowest...Ch. 7 - A car moves at speed v across a bridge made in the...Ch. 7 - Keratinocytes are the most common cells in the...Ch. 7 - Because of Earths rotation about its axis, a point...Ch. 7 - A roller coaster travels in a circular path, (a)...Ch. 7 - In Robert Heinleins The Moon Is a Harsh Mistress,...Ch. 7 - A model airplane of mass 0.750 kg flies with a...Ch. 7 - In a home laundry dryer, a cylindrical tub...Ch. 7 - Casting of molten metal is important in many...Ch. 7 - A skier starts at rest at the top of a large...Ch. 7 - A stuntman whose mass is 70 kg swings from the end...Ch. 7 - Suppose a 1 800-kg car passes over a bump in a...Ch. 7 - The pilot of an airplane executes a constant-speed...Ch. 7 - Prob. 67APCh. 7 - A coin rests 15.0 cm from the center of a...Ch. 7 - A 4.0-kg object is attached to a vertical rod by...Ch. 7 - A 0.275-kg object is swung in a vertical circular...Ch. 7 - (a) A luggage carousel at an airport has the form...Ch. 7 - The maximum lift force on a bat is proportional to...Ch. 7 - In a popular amusement park ride, a rotating...Ch. 7 - A massless spring of constant k = 78.4 N/m is...Ch. 7 - A 0.50-kg ball that is tied to the end of a 1.5-m...
Additional Science Textbook Solutions
Find more solutions based on key concepts
2. Which of the following is the best example of the use of a referent? _
a. A red bicycle
b. Big as a dump tru...
Physical Science
The validity of a scientific law.
Physical Universe
Why are scientists interested in the possibility of life beyond Earth?
Life in the Universe (4th Edition)
1. What are the temperatures for freezing water on the Celsius and the Fahrenheit scales, respectively? For boi...
Conceptual Physical Science (6th Edition)
Why doesnt Earths rotation provide a suitable time standard?
Essential University Physics (3rd Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- There is a CD-rom that's spinning a CD at 2,000 rpm. There is a bit of dirt, weighing 0.220 g, attached to the CD 3.50 cm from the centre. What must the force of friction between the CD and the dirt be so that the bit of dirt continues to rotate in a circle and doesn't fly off? Give your answers in units of mN (millinewton), to three significant figuresarrow_forwardAt takeoff, a commercial jet has a 45.00 m/s speed. Its tires have a diameter of 0.400 m. (a) At how many rev/min are the tires rotating? (b) What is the centripetal acceleration at the edge of the tire? (c) With what force must a determined 1.00×10−15 kg1.00×10−15 kg bacterium cling to the rim? (d) Take the ratio of this force to the bacterium's weight.arrow_forwardAn air puck of mass m1 = 0.25 kg is tied to a siring and allowed to revolve in a circle of radius R = 1.0 m on a frictionless horizontal table. The other end of the string passes through a hole in the center of the table, and a mass of m2 = 1.0 kg is tied to it (Fig. P7.27). The suspended mass remains in equilibrium while the puck on the tabletop revolves, (a) What is the tension in the string? (b) What is the horizontal force acting on the puck? (c) What is the speed of the puck? Figure P7.27arrow_forward
- Why is the following situation impossible? A mischievous child goes to an amusement park with his family. On one ride, after a severe scolding from his mother, he slips out of his seat and climbs to the top of the rides structure, which is shaped like a cone with its axis vertical and its sloped sides making an angle of = 20.0 with the horizontal as shown in Figure P6.32. This part of the structure rotates about the vertical central axis when the ride operates. The child sits on the sloped surface at a point d = 5.32 m down the sloped side from the center of the cone and pouts. The coefficient of static friction between the boy and the cone is 0.700. The ride operator does not notice that the child has slipped away from his seat and so continues to operate the ride. As a result, the sitting, pouting boy rotates in a circular path at a speed of 3.75 m/s. Figure P6.32arrow_forwardA ball of mass m = 0.275 kg swings in a vertical circular path on a string L = 0.850 in long as in Figure P6.31. (a) What are the forces acting on the ball at any point on the path? (b) Draw force diagrams for the ball when it is at the bottom of the circle and when it is at the top. (c) If its speed is 5.20 m/s at the top of the circle, what is the tension in the string there? (d) If the string breaks when its tension exceeds 22.5 N, what is the maximum speed the ball can have at the bottom before that happens? Figure P6.31arrow_forwardA light string can support a stationary hanging load of 25.0 kg before breaking. An object of mass m = 3.00 kg attached to the string rotates on a frictionless, horizontal table in a circle of radius r = 0.800 m, and the other end of the string is held fixed as in Figure P5.17. What range of speeds can the object have before the string breaks? Figure P5.17arrow_forward
- Why is the following situation impossible? The object of mass m = 4.00 kg in Figure P5.18 is attached to a vertical rod by two strings of length = 2.00 m. The strings are attached to the rod at points a distance d = 3.00 m apart. The object rotates in a horizontal circle at a constant speed of v = 3.00 m/s, and the strings remain taut. The rod rotates along with the object so that the strings do not wrap on to the rod. What If? Could this situation be possible on another planet?arrow_forwardInstead of moving back and forth, a conical pendulum moves in a circle at constant speed as its string traces out a cone (Fig. P6.68). One such pendulum is constructed with a string of length L = 12.0cm and bob of mass 0.210 kg. The string makes an angle = 7.00 with the vertical, a. What is the radial acceleration of the bob? b. What are the horizontal and vertical components of the tension force exerted by the string on the bob?arrow_forwardAn air puck of mass m1 = 0.25 kg is tied to a siring and allowed to revolve in a circle of radius R = 1.0 m on a frictionless horizontal table. The other end of the string passes through a hole in the center of the table, and a mass of m2 = 1.0 kg is tied to it (Fig. P7.27). The suspended mass remains in equilibrium while the puck on the tabletop revolves, (a) What is the tension in the string? (b) What is the horizontal force acting on the puck? (c) What is the speed of the puck? Figure P7.27arrow_forward
- Banked curves are designed so that the radial component of the normal force on the car rounding the curve provides the centripetal force required to execute uniform circular motion and safely negotiate the curve. A car rounds a banked curve with banking angle = 22.0 and radius of curvature 150 m. a. If the coefficient of static friction between the cars tires and the road is s = 0.400, what is the range of speeds for which the car can safely negotiate the turn without slipping? b. What is the minimum value of s for which the cars minimum safe speed is zero? Note that friction points up the incline here.arrow_forwardA puck of mass m=0.075 kgis moving in a circle on a horizontal frictionless surface. It is held in its path by a massless string of length L=0.42 m. The puck makes one revolution every t=0.35 s a)What is the magnitude of the tension in the string, in newtons, while the puck revolves? b)arrow_forwardA 700 kg car rounds a curve that is banked with an angle of 10 degrees from the horizontal and has a radius 50 meters. There is friction between the road and the tires and the maximum static frictional force is 3820 N. The normal force on the car while it goes around the curve is 7640 N. What maximum speed can the car take the turn without slipping a)24 m/s b)36 m/s c)18 m/s d)42 m/sarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning

College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Glencoe Physics: Principles and Problems, Student...
Physics
ISBN:9780078807213
Author:Paul W. Zitzewitz
Publisher:Glencoe/McGraw-Hill

Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
What Is Circular Motion? | Physics in Motion; Author: GPB Education;https://www.youtube.com/watch?v=1cL6pHmbQ2c;License: Standard YouTube License, CC-BY