Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter3: Functions And Graphs
Section3.7: Operations On Functions
Problem 2E
Related questions
Concept explainers
Riemann Sum
Riemann Sums is a special type of approximation of the area under a curve by dividing it into multiple simple shapes like rectangles or trapezoids and is used in integrals when finite sums are involved. Figuring out the area of a curve is complex hence this method makes it simple. Usually, we take the help of different integration methods for this purpose. This is one of the major parts of integral calculus.
Riemann Integral
Bernhard Riemann's integral was the first systematic description of the integral of a function on an interval in the branch of mathematics known as real analysis.
Question
Using trigonometric substitution calculate the integral of x√(1+x^2)dx
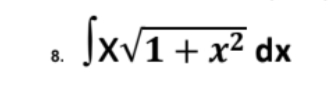
Transcribed Image Text:JxV1+ x² dx
8.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning