A B C - 3 m -- 3 m 6 m (a) B -2 (b) Influence Line for Sc (kN/kN) (e) Influence Line for Mc (kN-m/kN) 90 kN 90 kN 20 kN/m Just to the right of C 40 kN/m 40 kN/m 40 kN/m IT 60 kN/m 20 KN/m 60 kN/m DA A B C A (c) Loading Arrangement for Maximum Positive Sc (f) Loading Arrangement for Maximum Positive Mc 90 kN Just to the left of C 90 kN 40 kN/mf 20 kN/m -||| 40 kN/n 20 kN/m 20 kN/m 60 kN/m – B C B C A De A D (d) Loading Arrangement for Maximum Negative Se (g) Loading Arrangement for Maximum Negative Mc FIG. 9.5
A B C - 3 m -- 3 m 6 m (a) B -2 (b) Influence Line for Sc (kN/kN) (e) Influence Line for Mc (kN-m/kN) 90 kN 90 kN 20 kN/m Just to the right of C 40 kN/m 40 kN/m 40 kN/m IT 60 kN/m 20 KN/m 60 kN/m DA A B C A (c) Loading Arrangement for Maximum Positive Sc (f) Loading Arrangement for Maximum Positive Mc 90 kN Just to the left of C 90 kN 40 kN/mf 20 kN/m -||| 40 kN/n 20 kN/m 20 kN/m 60 kN/m – B C B C A De A D (d) Loading Arrangement for Maximum Negative Se (g) Loading Arrangement for Maximum Negative Mc FIG. 9.5
Residential Construction Academy: House Wiring (MindTap Course List)
5th Edition
ISBN:9781337402415
Author:Gregory W Fletcher
Publisher:Gregory W Fletcher
Chapter12: Raceway Installation
Section: Chapter Questions
Problem 14RQ
Related questions
Question
For the beam shown in Fig. 9.5(a), determine the maximum positive and negative shears and the maximum positive and negative bending moments at point C due to a concentrated live load of 90 kN, a uniformly distributed live load of 40 kN/m, and a uniformly distributed dead load of 20 kN/m.
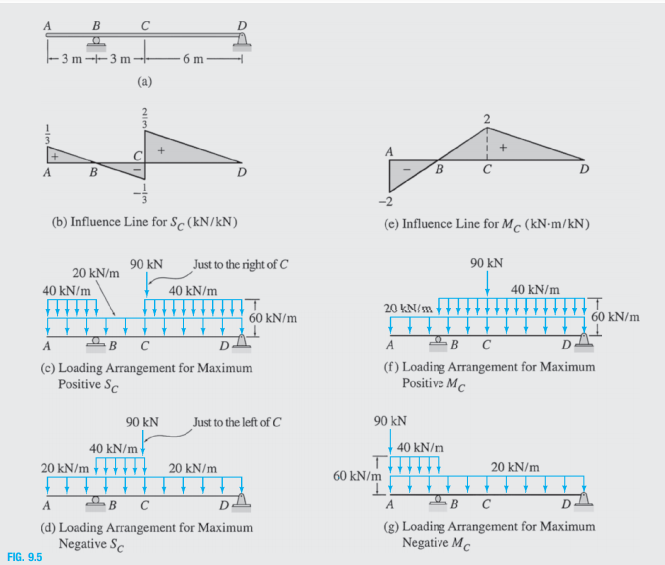
Transcribed Image Text:A
B
C
- 3 m -- 3 m
6 m
(a)
B
-2
(b) Influence Line for Sc (kN/kN)
(e) Influence Line for Mc (kN-m/kN)
90 kN
90 kN
20 kN/m
Just to the right of C
40 kN/m
40 kN/m
40 kN/m
IT
60 kN/m
20 KN/m
60 kN/m
DA
A
B C
A
(c) Loading Arrangement for Maximum
Positive Sc
(f) Loading Arrangement for Maximum
Positive Mc
90 kN
Just to the left of C
90 kN
40 kN/mf
20 kN/m -|||
40 kN/n
20 kN/m
20 kN/m
60 kN/m
– B C
B C
A
De
A
D
(d) Loading Arrangement for Maximum
Negative Se
(g) Loading Arrangement for Maximum
Negative Mc
FIG. 9.5
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Residential Construction Academy: House Wiring (M…
Civil Engineering
ISBN:
9781337402415
Author:
Gregory W Fletcher
Publisher:
Cengage Learning

Residential Construction Academy: House Wiring (M…
Civil Engineering
ISBN:
9781337402415
Author:
Gregory W Fletcher
Publisher:
Cengage Learning