Math
GeometryElementary Geometry for College StudentsFor Figure (a) of Exercise 1, find the number of faces, vertices, and edges in the polyhedron. Then verify Euler’s equation for that polyhedron.
close solutoin list

For Figure (a) of Exercise 1, find the number of faces, vertices, and edges in the polyhedron. Then verify Euler’s equation for that polyhedron.

BuyFind

Elementary Geometry for College St...

6th Edition
Daniel C. Alexander + 1 other
Publisher: Cengage Learning
ISBN: 9781285195698
BuyFind

Elementary Geometry for College St...

6th Edition
Daniel C. Alexander + 1 other
Publisher: Cengage Learning
ISBN: 9781285195698

Solutions

Chapter
Section
Problem 1E
Problem 2E
Problem 3E
Problem 4E
Problem 5E
Problem 6E
Problem 7E
Problem 8E
Problem 9E
Problem 10E
Problem 11E
Problem 12E
Problem 13E
Problem 14E
Problem 15E
Problem 16E
Problem 17E
Problem 18E
Problem 19E
Problem 20E
Problem 21E
Problem 22E
Problem 23E
Problem 24E
Problem 25E
Problem 27E
Problem 28E
Problem 29E
Problem 30E
Problem 31E
Problem 32E
Problem 33E
Problem 34E
Problem 35E
Problem 36E
Problem 37E
Problem 38E
Problem 39E
Problem 40E
Problem 41E
Problem 42E
Problem 43E
Problem 44E
Problem 45E
Problem 46E
Problem 47E
Problem 48E
Problem 49E
Problem 50E
Chapter 9.4, Problem 2E
Textbook Problem

Chapter 9.4, Problem 2E, For Figure a of Exercise 1, find the number of faces, vertices, and edges in the polyhedron. Then

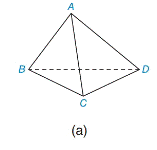
For Figure (a) of Exercise 1, find the number of faces, vertices, and edges in the polyhedron. Then verify Euler’s equation for that polyhedron.

Expert Solution

Want to see the full answer?

Check out a sample textbook solution.See solution
Chapter 9.4,
Problem 1E
Chapter 9.4,
Problem 3E

Want to see this answer and more?

Experts are waiting 24/7 to provide step-by-step solutions in as fast as 30 minutes!*

See Solution

*Response times vary by subject and question complexity. Median response time is 34 minutes and may be longer for new subjects.

Chapter 9 Solutions

Elementary Geometry for College Students
Show all chapter solutions
Ch. 9.1 - Consider the solid shown. a Does it appear to be a...Ch. 9.1 - Consider the solid shown. a Does it appear to be a...Ch. 9.1 - Consider the hexagonal prism shown in Exercise 1....Ch. 9.1 - Consider the triangular prism shown in Exercise 2....Ch. 9.1 - If each edge of the hexagonal prism in Exercise 1...Ch. 9.1 - If each edge of the triangular prism in Exercise...Ch. 9.1 - Suppose that each of the bases of the hexagonal...Ch. 9.1 - Suppose that each of the bases of the triangular...Ch. 9.1 - Suppose that each of bases of the hexagonal prism...Ch. 9.1 - Suppose that each of the bases of the triangular...
Ch. 9.1 - A solid is an octagonal prism. a How many vertices...Ch. 9.1 - A solid is a pentagonal prism. a How many vertices...Ch. 9.1 - Generalize the results found in Exercise 11 and 12...Ch. 9.1 - In the accompanying regular pentagonal prism,...Ch. 9.1 - In the regular pentagonal prism shown above,...Ch. 9.1 - For the right triangular prism, suppose that the...Ch. 9.1 - For the right triangular prism found in Exercise...Ch. 9.1 - Given that 100 cm =1 m, find the number of cubic...Ch. 9.1 - Given that 12 in. =1 ft, find the number of cubic...Ch. 9.1 - Find the volume and the surface area of a closed...Ch. 9.1 - Find the volume and the surface area of a closed...Ch. 9.1 - A cereal box measures 2 in. by 8 in. by 10 in....Ch. 9.1 - The measures of the sides of the square base of a...Ch. 9.1 - For a given box, the height measures 4 m. If the...Ch. 9.1 - For the box shown, the total area is 94 cm2....Ch. 9.1 - If the volume of the box is 252 in3, find the...Ch. 9.1 - The box with dimensions indicated is to be...Ch. 9.1 - A hollow steel door is 32 in. wide by 80 in. tall...Ch. 9.1 - A storage shed is in the shape of a pentagonal...Ch. 9.1 - A storage shed is in the shape of a trapezoidal...Ch. 9.1 - A cube is a right square prism in which all edges...Ch. 9.1 - Use the formulas and drawing in Exercise 31 to...Ch. 9.1 - When the length of each edge of a cube is...Ch. 9.1 - The numerical value of the volume of a cube equals...Ch. 9.1 - The sum of the lengths of all edges of a cube is...Ch. 9.1 - A concrete pad 4 in. thick is to have a length of...Ch. 9.1 - Zaidah plans a raised flower bed 2 ft high by 12...Ch. 9.1 - In excavating for a new house, a contractor digs a...Ch. 9.1 - Kristine creates an open box by cutting congruent...Ch. 9.1 - As in Exercise 39, find the volume of the box if...Ch. 9.1 - Kiannas aquarium is box-shaped with dimensions of...Ch. 9.1 - The gasoline tank on an automobile is box-shaped...Ch. 9.1 - For Exercise 43 to 45, consider the oblique...Ch. 9.1 - For Exercise 43 to 45, consider the oblique...Ch. 9.1 - For Exercise 43 to 45, consider the oblique...Ch. 9.1 - It can be shown that the length of a diagonal of a...Ch. 9.1 - A diagonal of a cube joins two vertices so that...Ch. 9.2 - In Exercises 1 to 4, name the solid that is shown....Ch. 9.2 - In Exercises 1 to 4, name the solid that is shown....Ch. 9.2 - In Exercises 1 to 4, name the solid that is shown....Ch. 9.2 - In Exercises 1 to 4, name the solid that is shown....Ch. 9.2 - In the solid shown, base ABCD is a square. a Is...Ch. 9.2 - In the solid on page 406, the base is a regular...Ch. 9.2 - Consider the square pyramid in Exercise 5. a How...Ch. 9.2 - Consider the hexagonal pyramid in Exercise 6. a...Ch. 9.2 - Suppose that the lateral faces of the pyramid in...Ch. 9.2 - Suppose that the base of the hexagonal pyramid in...Ch. 9.2 - Suppose that the base of the square pyramid in...Ch. 9.2 - Suppose that the base of the hexagonal pyramid in...Ch. 9.2 - Assume that the number of sides in the base of a...Ch. 9.2 - Refer to the prisms of Exercises 1 and 2. Which of...Ch. 9.2 - Refer to the pyramids of Exercises 3 and 4. Which...Ch. 9.2 - Refer to the prisms of Exercises 1 and 2. Which of...Ch. 9.2 - Refer to the pyramids of Exercises 3 and 4. Which...Ch. 9.2 - Consider any regular pyramid. Indicate which line...Ch. 9.2 - Consider any regular pyramid. Indicate which line...Ch. 9.2 - In Exercises 20 and 21, use Theorem 9.2.1 in which...Ch. 9.2 - In Exercises 20 and 21, use Theorem 9.2.1 in which...Ch. 9.2 - In a regular pentagonal pyramid, each lateral edge...Ch. 9.2 - In a regular pentagonal pyramid, each base edge...Ch. 9.2 - For the regular square pyramid shown, suppose that...Ch. 9.2 - For the regular square pyramid shown in Exercise...Ch. 9.2 - The figure below is a regular hexagonal pyramid. a...Ch. 9.2 - For a regular square pyramid, suppose that the...Ch. 9.2 - For a regular square pyramid, the slant height of...Ch. 9.2 - A church steeple in the shape of a regular square...Ch. 9.2 - Before the shingles of the steeple see Exercise 29...Ch. 9.2 - A teepee is constructed by using 12 poles. The...Ch. 9.2 - For its occupants to be protected from the...Ch. 9.2 - The street departments storage building, which is...Ch. 9.2 - The foyer planned as an addition to an existing...Ch. 9.2 - The exhaust chute on a wood chipper has a shape...Ch. 9.2 - A popcorn container at a movie theatre has the...Ch. 9.2 - A regular tetrahedron is a regular triangular...Ch. 9.2 - Each edge of a regular tetrahedron see Exercise 37...Ch. 9.2 - Exercise 39 and 40 are based upon the uniqueness...Ch. 9.2 - Exercise 39 and 40 are based upon the uniqueness...Ch. 9.2 - Consider the accompanying figure. When the four...Ch. 9.2 - Find the volume of the regular square pyramid that...Ch. 9.2 - Where e1 and e2 are the lengths of two...Ch. 9.2 - Use the information from Exercise 43 to find the...Ch. 9.2 - A hexagonal pyramid not regular with base ABCDEF...Ch. 9.3 - Does a right circular cylinder such as an aluminum...Ch. 9.3 - Does a right circular cone such as a wizards cap...Ch. 9.3 - For the right circular cylinder shown on page 471,...Ch. 9.3 - For the right circular cylinder shown on page 417,...Ch. 9.3 - For the right circular cylinder, suppose that r=5...Ch. 9.3 - Suppose that r=12 cm and h=15 cm in the right...Ch. 9.3 - The tin can shown at the right has the indicated...Ch. 9.3 - What is the volume of the tin can? If it contains...Ch. 9.3 - If the exact volume of a right circular cylinder...Ch. 9.3 - Suppose that the volume of an aluminum can is to...Ch. 9.3 - For an aluminum can, the lateral surface area is...Ch. 9.3 - Find the height of a storage tank in the shape of...Ch. 9.3 - Find the volume of the oblique circular cylinder....Ch. 9.3 - A cylindrical orange juice container has metal...Ch. 9.3 - In Exercises 15 to 20, use that fact that r2+h2=l2...Ch. 9.3 - In Exercises 15 to 20, use that fact that r2+h2=l2...Ch. 9.3 - In Exercises 15 to 20, use that fact that r2+h2=l2...Ch. 9.3 - In Exercises 15 to 20, use that fact that r2+h2=l2...Ch. 9.3 - In Exercises 15 to 20, use that fact that r2+h2=l2...Ch. 9.3 - In Exercises 15 to 20, use that fact that r2+h2=l2...Ch. 9.3 - The oblique circular cone has an altitude and a...Ch. 9.3 - For the accompanying right circular cone, h=6 m...Ch. 9.3 - For the right circular cone shown in Exercise 22,...Ch. 9.3 - Rukia discovers that the teepee with a circular...Ch. 9.3 - A rectangle has dimensions of 6 in. by 3 in. Find...Ch. 9.3 - A rectangle has dimensions of 6in. by 3 in. Find...Ch. 9.3 - A triangle has sides that measure 15 cm, 20 cm,...Ch. 9.3 - A triangle has sides that measure 15 cm, 20 cm,...Ch. 9.3 - A triangle has sides that measure 15 cm, 20 cm,...Ch. 9.3 - Where r is the length of the radius of a sphere,...Ch. 9.3 - If a right circular cone has a circular base with...Ch. 9.3 - A right circular cone has a slant height of 12 ft...Ch. 9.3 - A solid is formed by cutting a conical section...Ch. 9.3 - In Exercises 34 and 35, give a paragraph proof for...Ch. 9.3 - In Exercises 34 and 35, give a paragraph proof for...Ch. 9.3 - For a right circular cone, the slant height has a...Ch. 9.3 - For a right circular cone, the ratio of the slant...Ch. 9.3 - If the length of the radius and the height of a...Ch. 9.3 - For the two similar cylinders in Exercise 38, what...Ch. 9.3 - For a right circular cone, the dimensions are r=6...Ch. 9.3 - A cylindrical storage tank has a depth of 5 ft and...Ch. 9.3 - If the tank in Exercises 41 needs to be painted...Ch. 9.3 - A frustum of a cone is the portion of the cone...Ch. 9.3 - In Exercises 44 and 45, use the formula from...Ch. 9.3 - In Exercises 44 and 45, use the formula from...Ch. 9.3 - An oil refinery has storage tanks in the shape of...Ch. 9.3 - A farmer has a fuel tank in the shape of a right...Ch. 9.3 - When radii OA and OB are placed so that they...Ch. 9.3 - A lawn roller in the shape of a right circular...Ch. 9.4 - Which of these two polyhedrons is concave? Note...Ch. 9.4 - For Figure a of Exercise 1, find the number of...Ch. 9.4 - For figure b of Exercise 1, find the number of...Ch. 9.4 - For a regular tetrahedron, find the number of...Ch. 9.4 - For a regular hexahedron, find the number of...Ch. 9.4 - A regular polyhedron has 12 edges and 8 vertices....Ch. 9.4 - A regular polyhedron has 12 edges and 6 vertices....Ch. 9.4 - A polyhedron not regular has 10 vertices and 7...Ch. 9.4 - A polyhedron not regular has 14 vertices and 21...Ch. 9.4 - In Exercises 10 to 12, the probability is the...Ch. 9.4 - In Exercises 10 to 12, the probability is the...Ch. 9.4 - In Exercises 10 to 12, the probability is the...Ch. 9.4 - In sphere O, the length of radius OP- is 6 in....Ch. 9.4 - Find the approximate surface area and volume of...Ch. 9.4 - Find the total area surface area of a regular...Ch. 9.4 - Find the total area surface area of a regular...Ch. 9.4 - Find the total area surface area of a regular...Ch. 9.4 - Find the total area surface area of a regular...Ch. 9.4 - The total area surface area of a regular...Ch. 9.4 - The total area surface area of a regular...Ch. 9.4 - Find the approximate volume of a sphere with...Ch. 9.4 - Find the approximate volume of a sphere with...Ch. 9.4 - The surface of a soccer ball is composed of 12...Ch. 9.4 - A calendar is determined by using each of the 12...Ch. 9.4 - A sphere is inscribed within a right circular...Ch. 9.4 - In calculus, it can be shown that the largest...Ch. 9.4 - Given that a regular polyhedron of n faces is...Ch. 9.4 - A right circular cone is inscribed in a sphere. If...Ch. 9.4 - A sphere is inscribed in a right circular cone...Ch. 9.4 - In Exercises 31 and 32, use the calculator value...Ch. 9.4 - In Exercises 31 and 32, use the calculator value...Ch. 9.4 - A sphere has a volume equal to 997in3. Determine...Ch. 9.4 - A sphere has a surface area equal to 154in2....Ch. 9.4 - The spherical storage tank described in Example 5...Ch. 9.4 - An observatory has the shape of a right circular...Ch. 9.4 - A leather soccer ball has an inside diameter...Ch. 9.4 - An ice cream cone is filled with ice cream as...Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - For Exercises 39 to 44, make drawings as needed....Ch. 9.4 - Suppose that a semicircular region with a vertical...Ch. 9.4 - Suppose that a semicircular region with vertical...Ch. 9.4 - Sketch the torus that results when the given...Ch. 9.4 - Sketch the solid that results when the given...Ch. 9.4 - Explain how the following formula used in Example...Ch. 9.4 - Derive a formula for the total surface area of the...Ch. 9.CR - Each side of the base of a right octagonal prism...Ch. 9.CR - The base of a right prism is a triangle whose...Ch. 9.CR - The height of a square box is 2 in. more than...Ch. 9.CR - The base of a right prism is a rectangle whose...Ch. 9.CR - The base of a right prism is a triangle whose...Ch. 9.CR - The base of a right prism is a regular hexagon...Ch. 9.CR - A regular square pyramid has a base whose sides...Ch. 9.CR - A regular hexagonal pyramid has a base whose sides...Ch. 9.CR - The radius of the base of a right circular cone...Ch. 9.CR - The diameter of the base of a right circular cone...Ch. 9.CR - The slant height of a regular square pyramid...Ch. 9.CR - The base of a regular pyramid is an equilateral...Ch. 9.CR - The radius length of the base of a right circular...Ch. 9.CR - a For the through in the shape of half-cylinder,...Ch. 9.CR - The slant height of a right circular cone is 12...Ch. 9.CR - The volume of the right circular cone is 96 in. If...Ch. 9.CR - Find the surface area of a sphere if the radius...Ch. 9.CR - Find the volume of a sphere if the diameter has...Ch. 9.CR - The solid shown consists of a hemisphere half of a...Ch. 9.CR - If the radius length of one sphere is three times...Ch. 9.CR - Find the volume of the solid of revolution that...Ch. 9.CR - Find the exact volume of the solid of revolution...Ch. 9.CR - Find the exact volume of the solid of revolution...Ch. 9.CR - A plastic pipe is 3 ft long and has an inside...Ch. 9.CR - A sphere with a diameter length of 14 in. is...Ch. 9.CR - a An octahedron has _________________ faces that...Ch. 9.CR - A drug manufacturing company wants to manufacture...Ch. 9.CR - For each of the following solids, verify Eulers...Ch. 9.CR - Find the volume of cement used in the block shows.Ch. 9.CR - Given a die in the shape of a regular octahedron,...Ch. 9.CR - Find the total surface area of a a regular...Ch. 9.CR - Three spheres are externally tangent to each other...Ch. 9.CT - For the regular pentagonal prism shown below, find...Ch. 9.CT - For the regular pentagonal base, each edge...Ch. 9.CT - For the regular square pyramid shown, find the...Ch. 9.CT - For the regular square pyramid shown above, find a...Ch. 9.CT - For the regular square pyramid shown, find the...Ch. 9.CT - Find the height of the regular square pyramid...Ch. 9.CT - Find the volume of the regular square pyramid...Ch. 9.CT - Determine whether the statement is true or false....Ch. 9.CT - Determine whether the statement is true or false....Ch. 9.CT - Recall Eulers equations, V+F=E+2. For a certain...Ch. 9.CT - Find the slant height of the right circular cone...Ch. 9.CT - For the right circular cylinder shown, r=4 cm and...Ch. 9.CT - The exact volume of a right circular cone not...Ch. 9.CT - Assume that a die used for gaming is in the shape...Ch. 9.CT - A spherical storage tank filled with water has a...Ch. 9.CT - A pump moves water at a rate of 8ft3 per minute....

Additional Math Textbook Solutions

Find more solutions based on key concepts
Show solutions
Evaluate dy if y = x3 2x2 + 1, x = 2, and dx = 0.2.

Single Variable Calculus: Early Transcendentals, Volume I

Find the work done by the force F = 3i 5j in moving an object from the point (2, 2) to the point (7, 13).

Precalculus: Mathematics for Calculus (Standalone Book)

The graphs of f and g are given. (a) State the values of f(4) and g(3). (b) For what values of x is f(x) = g(x)...

Single Variable Calculus

Solve each equation in Exercises 107120 for x, rounding your answer to four significant digits where necessary....

Finite Mathematics and Applied Calculus (MindTap Course List)

a. SOC Statewide, the population as a whole watches 6.2 hours of TV per day. A random sample of 1017 senior cit...

Essentials Of Statistics

Find the vertices, foci, and asymptotes of the hyperbola and sketch its graph. 24. 9y2 4x2 36y 8x = 4

Multivariable Calculus

Simplify: 2736

Elementary Technical Mathematics

Interpretation: Test of Independence Consider Charlotte's study of source of fraud/identity theft and gender (s...

Understanding Basic Statistics

In Exercises 4756, solve the given equation for the indicated variable. 1,000=500(1.12t) (Round the answer to f...

Applied Calculus

Find the limits as x and as x . Use this information, together with intercepts, to give a rough sketch of th...

Calculus: Early Transcendentals

Consider purchasing a system of audio components consisting of a receiver, a pair of speakers, and a CD player....

Probability and Statistics for Engineering and the Sciences

Think About It Determine whether the function f(x)=0 is even, odd. both, or neither. Explain.

Calculus: Early Transcendental Functions

Determining Whether a Function is one-to-one In Exercises 5762, use a graphing utility to graph the function. T...

Calculus: An Applied Approach (MindTap Course List)

Oishi and Schimmk (2010) report that people who move from home to home frequently as children tend to have lowe...

Statistics for The Behavioral Sciences (MindTap Course List)

A lax form asks people to identify their age. annual income, number of dependents, and social security number. ...

Essentials of Statistics for The Behavioral Sciences (MindTap Course List)

Solve the equations in Exercises 126. 2x3x12x+3x+1=0

Finite Mathematics

For Problems 51-78, simplify each of the numerical expressions. Objective 3 493531812

Intermediate Algebra

In Exercises 5-8, plot the graph of the function f in an appropriate viewing window. (Note: The answer is not u...

Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach

Use inductive reasoning to predict the next symbol in the following list. Hint: Look for a pattern that involve...

Mathematical Excursions (MindTap Course List)

In problems 15-26, evaluate each expression. 24.

Mathematical Applications for the Management, Life, and Social Sciences

The region bounded by the curve y=1/(1+ex), the x- and y-axes, and the line x=10 is rotated about the x-axis. U...

Calculus (MindTap Course List)

If the radius of convergence of the power series n=0cnxn is 10, what is the radius of convergence of the series...

Single Variable Calculus: Early Transcendentals

Finding the Interval of Convergence In Exercises 4144, find the interval of convergence of the power series, wh...

Calculus of a Single Variable

Label each of the following statements as either true or false. The only ideals of the set of real numbers are...

Elements Of Modern Algebra

Last week you worked 18 hours and earned $256.50. What was your hourly rate?

Contemporary Mathematics for Business & Consumers

Find the remaining sides of a 454590 triangle if the longest side is 4

Trigonometry (MindTap Course List)

The accompanying tree diagram represents an experiment consisting of two trials. In Exercises 9-13, use the dia...

Finite Mathematics for the Managerial, Life, and Social Sciences

Surface Area In Exercises 63-68, find the area of the surface generated by revolving the curve about each given...

Calculus: Early Transcendental Functions (MindTap Course List)

f(x)=2x2+1x+3 has slant asymptote(s): a) y = 2x b) y = x c) y = 2x and y = 2x d) f does not have slant asymptot...

Study Guide for Stewart's Single Variable Calculus: Early Transcendentals, 8th

Ward Doering Auto Sales is considering offering a special service contract that will coverthe total cost of any...

STATISTICS F/BUSINESS+ECONOMICS-TEXT

Write an equation of each circle in standard form and graph the circle. x2+y26x+4y=3

College Algebra (MindTap Course List)

Determine the total length of stock in inches required to make 35 bushings each 34.2 mm long. Allow 316 inch wa...

Mathematics For Machine Technology

Explain how the Pearson correlation describes the relationship between two variables and predicts the general a...

Research Methods for the Behavioral Sciences (MindTap Course List)

Each year, U.S. News and World Report publishes a ranking of U.S. business schools. The following data give the...

Introduction To Statistics And Data Analysis

Graphing a Parametric Surface In Exercises 1316, use a computer algebra system to graph the surface represented...

Calculus

Explain when a manipulation check is needed, describe what it is intended to accomplish, and identify a manipul...

Research Methods for the Behavioral Sciences (MindTap Course List)

Exercises 1-7 involve the information in Figure 9.113 on painting a room. 1.Create a PERT chart for painting a ...

Mathematics: A Practical Odyssey

Find the iterated integral for , where R is the first quadrant of the ellipse 4x2 + 9y2 = 36 and the transforma...

Study Guide for Stewart's Multivariable Calculus, 8th

In exercise 18 the data on price () and the overall score for six stereo headphones tested by Consumer Reports ...

Statistics for Business & Economics, Revised (MindTap Course List)

Using Partial Fractions In Exercises 3-20, use partial fractions to find the indefinite integral. 4x2+2x1x3+x2d...

Calculus (MindTap Course List)

HOW DO YOU SEE IT? Each figure shows a region of integration for the double integral Rf(x,y)dA. For each region...

Multivariable Calculus

Adding or Subtracting Polynomials In Exercises 17-24, add or subtract and write the result in standard form. t3...

College Algebra

The mean cost of domestic airfares in the United States rose to an all-time high of $385 per ticket (Bureau of ...

Modern Business Statistics with Microsoft Office Excel (with XLSTAT Education Edition Printed Access Card) (MindTap Course List)

Use the following information to answer the next 13 exercises: The data In Table 8.10 are the result of a rando...

Introductory Statistics

Reminder Round all answers to two decimal places unless otherwise indicated. Note Some of the formulas below us...

Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)

The graph of a solution of a second-order initial-value problem d2y/dx2 = f(x, y, y), y(2) = y0, y(2) = y1, is ...

A First Course in Differential Equations with Modeling Applications (MindTap Course List)

Obesity. Obesity is a risk factor for many health problems such as type 2 diabetes, high blood pressure, joint ...

Essentials Of Statistics For Business & Economics

For the following exercises, sketch the graph of the logarithmic function. Determine the domain, range, and ver...

Calculus Volume 1

Write a complete proof for Theorem 5.9.4.

Discrete Mathematics With Applications

bartleby
  • Contact Research (Essays)
  • High School Textbooks
  • Literature Guides
  • Essay Help
  • Mobile App
    • © 2021 bartleby. All Rights Reserved.