
To solve the below inequality in terms of intervals and illustrate the solution set on the real number line -
Answer to Problem 26E
The solution of the inequality is
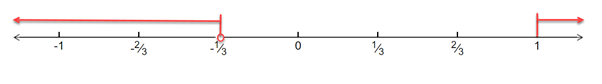
Explanation of Solution
Given: Inequality:
Formula Used:
An inequality compares two values, showing if one is less than, greater than, or simply not equal to another value.
Real number line is the line whose points are the real numbers.
Calculation:
Given: Inequality equation is
The above inequality can be broken down into:
Solving the first inequality, we have:
Adding
To solve the above inequality, we needto find the different intervals for which the inequality gives a value greater than
When
Thus,
So,
When
Thus,
So,
When
Thus,
So,
Combining all the solutions, we have the solution set as:
Solving the second inequality, we have:
Subtract
To solve the above inequality, we need to find the different intervals for which the inequality gives a value less than or equal to
When
Thus,
So,
When
Thus,
So,
When
Thus,
So,
When
Thus,
So,
When
Thus,
So,
Combining all the solutions, we have the solution set as:
Now, combining solutions from both the inequalities, we have:
Thus, solution set is
Drawing the above inequality on a real number line, we have:
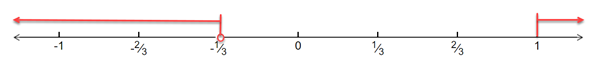
Conclusion:
Hence, the solution of the inequality is
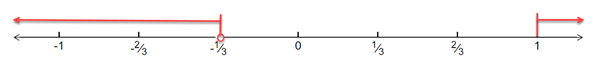
Chapter A Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





