Chapter C, Problem 30E

To determine

To calculate:

The value of $x$ to satisfy the following equation:

  $2{\sin }^{2}x=1$

Answer to Problem 30E

The values of $x$ for the interval $\left[0,2\pi \right]$ to satisfy eq. $2{\sin }^{2}x=1$ are $\frac{\pi }{4},\frac{3\pi }{4},\frac{5\pi }{4},\frac{7\pi }{4}$ .

Explanation of Solution

Given information:

  $\begin{array}{l}2{\sin }^{2}x=1\\ \left[0,2\pi \right]\end{array}$

Calculation:

Know that:

  $\begin{array}{l}2{\sin }^{2}x=1\\ {\sin }^{2}x=\frac{1}{2}\\ \sin x=\pm \frac{1}{\sqrt{2}}\end{array}$

Now, consider the values of $x$ in the given interval $\left[0,2\pi \right]$ that cause sine value is equal to $\pm \frac{1}{\sqrt{2}}$ .

Know that:

The circle has co-ordinates $\left(x,y\right)=\left(\cos \theta ,\sin \theta \right)$ with the radius $1$ .

Now, the angle corresponding to the $y$ co-ordinates means $\sin x=\pm \frac{1}{\sqrt{2}}$ , a unit circle is drawn as:

  

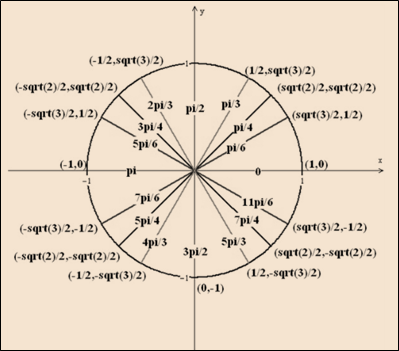
Fig. Unit circle of $\sin x=\pm \frac{1}{\sqrt{2}}$

From the diagram:

Sine is equal to $\pm \frac{1}{\sqrt{2}}$ when the angle is $\frac{\pi }{4},\frac{3\pi }{4},\frac{5\pi }{4},\frac{7\pi }{4}$ .

Therefore, the values of $x$ for the interval $\left[0,2\pi \right]$ to satisfy eq. $2{\sin }^{2}x=1$ are $\frac{\pi }{4},\frac{3\pi }{4},\frac{5\pi }{4},\frac{7\pi }{4}$ .