What is Thermodynamics?
Thermodynamics is the division of physics that deals with the transfer of any kind of energy, whether it be heat, temperature, or work, from one object to another.
Thermodynamics happens when an object comes in contact with a colder object and transfers heat to it, or when an object comes in contact with a hotter object and receives some heat from it.
What are the laws of thermodynamics?
The laws of thermodynamics help to examine the things that will be done and that will exist in real life. These laws were established after seeing their consequences on people and the environment. There are four laws of thermodynamics, which are given below.
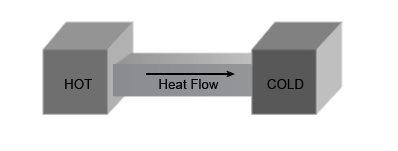
The Zeroth Law of Thermodynamics
According to this law, if the first body is in thermal equilibrium with the third body, and the second body is in thermal stability with the third body simultaneously, then the first and second body will be in thermal equilibrium with each other. The best example of this law is thermometers, as they are the third party in the scenario and help to find the body's temperature.
The First Law of Thermodynamics
This law is also recognized as the law of conservation of energy. According to this law, the variations that can be observed inside a system in terms of internal energy are equivalent to the difference of the work done by the person on their surroundings and the heat that is added to the person's body from the surroundings.
The Second Law of Thermodynamics
According to this law, heat cannot move from a cooler place to a hotter place spontaneously, and at a particular temperature, heat cannot be turned into work. The entropy of a closed place, or the heat energy per unit temperature, reaches the maximum value as time increases. All the closed systems obey the equilibrium state after a certain maximum value, and then after this, there is no energy left for accomplishing any task. The arrow of time is generated with the backward and forward movement of the processes, which is also in an asymmetric manner.
The Third Law of Thermodynamics
According to this law, the crystal's entropy, when it is in its most stable state, is zero as the temperature of the crystal reaches absolute zero. From the statistical point of view, the law allows us to build an absolute scale for establishing the entropy and helps to determine the degree of disorder or randomness of a system.
Thermodynamic relations
The types of thermodynamic relations are as follows:
- Maxwell relations
- Gibbs and Helmholtz function
- TDS equations
- Clausius–Clapeyron equation
Maxwell relations
The expression that correlates the partial derivatives of characteristics like pressure, volume, temperature, and entropy of an easy compressible system to each other is named Maxwell relations. A pure substance surviving in a single phase has only two independent variables of the eight quantities: pressure, volume, temperature, entropy, internal energy, enthalpy, Helmholtz function, and Gibb’s function, and one may be displayed as a function of any two others.
A pure substance experiencing a reversible process obeys the following equations:
(a)
(b)
(c)
(d)
In the above equations, U is the internal energy, T is the temperature, S is the entropy, p is the pressure, V is the volume, H is the enthalpy, F is the Helmholtz function, and G is the Gibbs function.
Since internal energy, enthalpy, Helmholtz function, and Gibb’s function are the thermodynamic properties and exact differential of the type:
Then, the solution of the above differential equation will be:
Applying this to all the above four differential equations:
These differential equations are named Maxwell relations. They are significant in thermodynamics because these equations present a means of determining the variation in entropy, which cannot be measured directly by simply measuring the changes in properties like pressure, volume, and temperature.
These relations are restricted to simple compressible systems. Though, other comparable relations can be addressed just as quickly for the non-simple systems, such as those involving electrical, magnetic, and other effects.
Gibbs and Helmholtz function
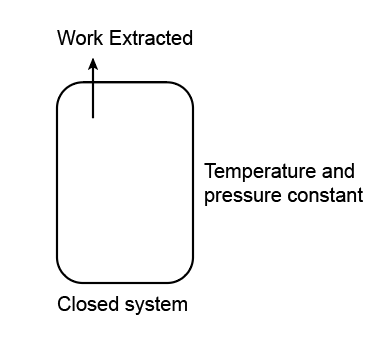
Josiah Willard Gibbs presented the theory of Gibbs free energy in the 1870s. Initially, he called the free energy of a system as its "available energy." He explained Gibb's free energy as the energy associated with a system that can further be utilized in doing work.
Gibb's free energy can be described as the amount of work that can be extracted from a closed system, given that its temperature and pressure are kept constant. If we show it mathematically, Gibbs free energy is depicted as the difference between the system enthalpy and the temperature-entropy product associated with it.
The following equation can represent the given statement:
This equation is termed the "Gibbs-Helmholtz equation".
Here are some valuable conclusions from the above equation:
- When the value of ΔG is negative, the reaction is spontaneous.
- When the value of ΔG is positive, the reaction is non-spontaneous.
- When it is zero, it shows that the process has struck equilibrium.
Gibbs free energy and the second law of thermodynamics
The second law of thermodynamics states that:
"During a process, the overall entropy is forced to undergo an extension, unless and until all the reactions included qualify as reversible."
Additionally, we can also provide specific pointers to better establish the given law:
- The spontaneous processes tend to be irreversible in their thermodynamic aspects.
- No system is capable of converting heat into work without any leakage of energy.
- Universal entropy is constantly bound to increase.
It is evident from the above statements that the second law of thermodynamics has a very definite relationship with the theory of Gibb's free energy. Obtaining insights from the two concepts, we can arrive at specific valuable conclusions. Let us consider one:
In a state where the change in enthalpy is negative, i.e., the enthalpy is decreasing for an irreversible process, the reaction will be spontaneous at all temperatures. It is because the entropy change will be positive.
TDS equations
There are two TDS equations. The first TDS equation is as follows:
Here, T is the temperature, S is the entropy, CV is the specific heat at constant volume, p is the pressure, and V is the volume.
The second TDS equation is as follows:
Here, Cp is the specific heat at constant pressure.
Either the first or second TDS equation can be applied to determine the change in the entropy of a system. The usual selection depends on the available data.
Clausius–Clapeyron equation
Clausius-Clapeyron expression correlates to variations in properties for a change of state of a substance whenever there is a variation of state, either from solid to liquid state or from liquid to vapor state, and the temperature remains constant, so long as the change is taking place. This temperature also relies on the pressure at which the change is taking place and on the property of each substance.
The Clausius–Clapeyron equation is as follows:
Here, L is the latent heat, V2 is the volume at the final state, and V1 is the volume at the initial state.
The Clausius–Clapeyron equation can be utilized to examine the change of saturation pressure with temperature, and it is also practiced in the solid vapor region by replacing hfg with hig (the enthalpy of sublimation) of the substance.
Common Mistakes
Students may get confused between enthalpy and entropy. Enthalpy is the addition of the flow energy and internal energy, while entropy is the determination of the randomness of molecules.
Another common point of confusion is between Gibbs free energy and standard free energy. Gibbs free energy is the thermodynamic quantity that is equivalent to enthalpy minus the product of entropy and absolute temperature, while the standard free energy is the quantity that gives Gibbs free energy at standard experimental conditions.
Context and Applications
The topic of thermodynamic relations is significant in the several professional exams and courses for the undergraduate, diploma, graduate, and postgraduate levels. For example:
- Bachelors in technology
- Bachelors in Science
- Masters in technology
- Masters in Science
Related Concepts
- Concept of internal energy
- Entropy
- Enthalpy
- Thermal equilibrium
- Heat transfer
Practice Problems
Q1: Maxwell’s equation consists of ___ equations.
(a) Three
(b) Nine
(c) Eight
(d) Four
Correct option: (d)
Explanation: Maxwell’s equation consists of four equations.
Q2: Among the four options, which of the following expressions defines the Helmholtz function F?
(a) F = H+TS
(b) F = H-TS
(c) F = U-TS
(d) F = U+TV
Correct option: (c)
Explanation: The expression for the Helmholtz function is F = U-TS.
Q3: The similar volume of all gases would represent their ________.
(a) Specific gravities
(b) Molecular weights
(c) Densities
(d) None of these
Correct option: (b)
Explanation: According to Avogadro's law, "same volume of all gases at the identical temperature and pressure, have the equal number of molecules.
Q4: The value of the work done in the free expansion process will be ________.
(a) Maximum
(b) Zero
(c) Negative
(d) Minimum
Correct option: (b)
Explanation: In the free expansion process, the value of the external pressure is zero. Thus, the work done will also be zero.
Q5: Which of the following quantities is not the property of the system?
(a) Heat
(b) Density
(c) Pressure
(d) Volume
Correct option: (a)
Explanation: Heat is a path function, not a property of the system.
Want more help with your mechanical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Thermodynamic Relations Homework Questions from Fellow Students
Browse our recently answered Thermodynamic Relations homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.