What is Acceleration Due to Gravity? 

In fundamental physics, gravity or gravitational force is the universal attractive force acting between all the matters that exist or exhibit. It is the weakest known force. Therefore no internal changes in an object occurs due to this force. On the other hand, it has control over the trajectories of bodies in the solar system and in the universe due to its vast scope and universal action. The free fall of objects on Earth and the motions of celestial bodies, according to Newton, are both determined by the same force. It was Newton who put forward that the moon is held by a strong attractive force exerted by the Earth which makes it revolve in a straight line. He was sure that this force is similar to the downward force which Earth exerts on all the objects on it.  

In Newton's theory, every tiny particle of matter attracts all other particles by gravity, and on this basis, he showed that the attraction of a finite body with spherical symmetry is the same as the attraction of any mass at the center of the body. More generally, the attraction of any free-falling body at a sufficiently large distance is equal to the attraction of the entire mass to the center of mass. Thus, he could relate two accelerations, the acceleration of the Moon and the acceleration of a body falling freely to the surface of the Earth, with a general interaction - the gravitational force between bodies, which decreases in proportion to the square of the distance between them. separate. So, if the distance between the bodies is doubled, the force acting on them decreases to a quarter of the original. 

The acceleration of a free-falling object falling is exerted by the net force which is directly proportional to the magnitude of the net force and inversely proportional to the mass of the object. This follows Newton's second law of motion which states the acceleration of a body depends on the net force and the mass of the body. 

Equations, Formula, and Explanation of Acceleration Due to Gravity: 

1. The circular orbital motion of a radius R rotating at a time period T, needs an inward acceleration A equal to product of the circumference 4π.2, the acceleration equation is $\text{A=}\frac{{\text{4Π}}^{\text{2}}\text{R}}{{\text{T}}^{\text{2}}}$

2. Newton's gravitational force equation is ${\text{F}}_{\text{12}}\text{=}\frac{{\text{GM}}_{\text{1}}{\text{M}}_{\text{2}}}{{\text{r}}_{\text{12}}{}^{\text{2}}}$. Here ${\text{F}}_{\text{12}}$ is the magnitude of the gravitational force, M1 and M2 are the masses of the two bodies, r12 is the distance between of separation between the two bodies and G is the universal gravitation constant. The equation can be rearranged to find the mass of one of the body, ${\text{M}}_{\text{2}}\text{=}\left({\text{F}}_{\text{2}}{\text{/F}}_{\text{1}}\right){\text{ × M}}_{\text{1}}$. As per the equivalence theory, the gravitational mass is equal to the inertial mass of the body. The universal gravitational constant G has its value $\text{6}{\text{.67×10}}^{\text{-11}}{\text{kg }}^{\text{-2}}{\text{m}}^{\text{2}}$, which depends on the physical quantities like length, mass and time taken to reach the ground.

3. The gravitational force is a vector quantity which acts in the direction of the two bodies, so let r be the vector quantity of the distance of the separation. So the gravitational force formula becomes $\text{F=}\frac{{\text{GM}}_{\text{1}}{\text{M}}_{\text{2}}\text{r}}{{\text{r}}^{\text{3}}}$, so the simplified equation becomes $\text{F=}\frac{{\text{GM}}_{\text{1}}{\text{M}}_{\text{2}}}{{\text{r}}^2}$

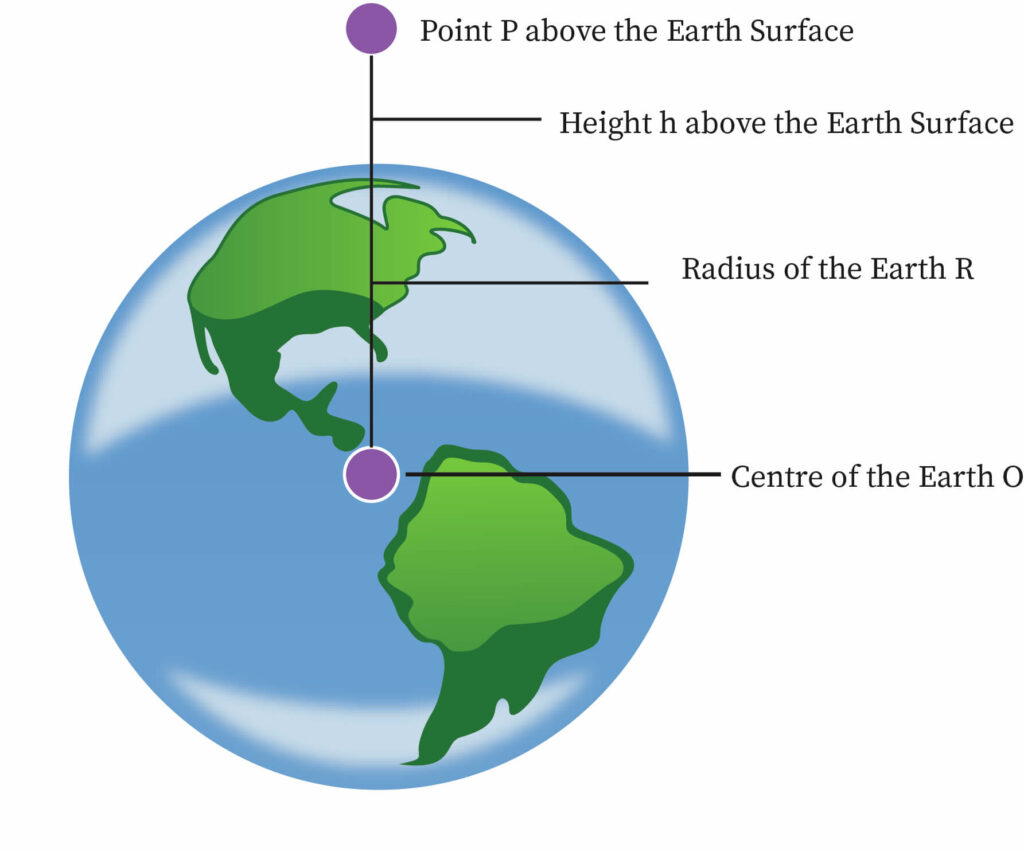
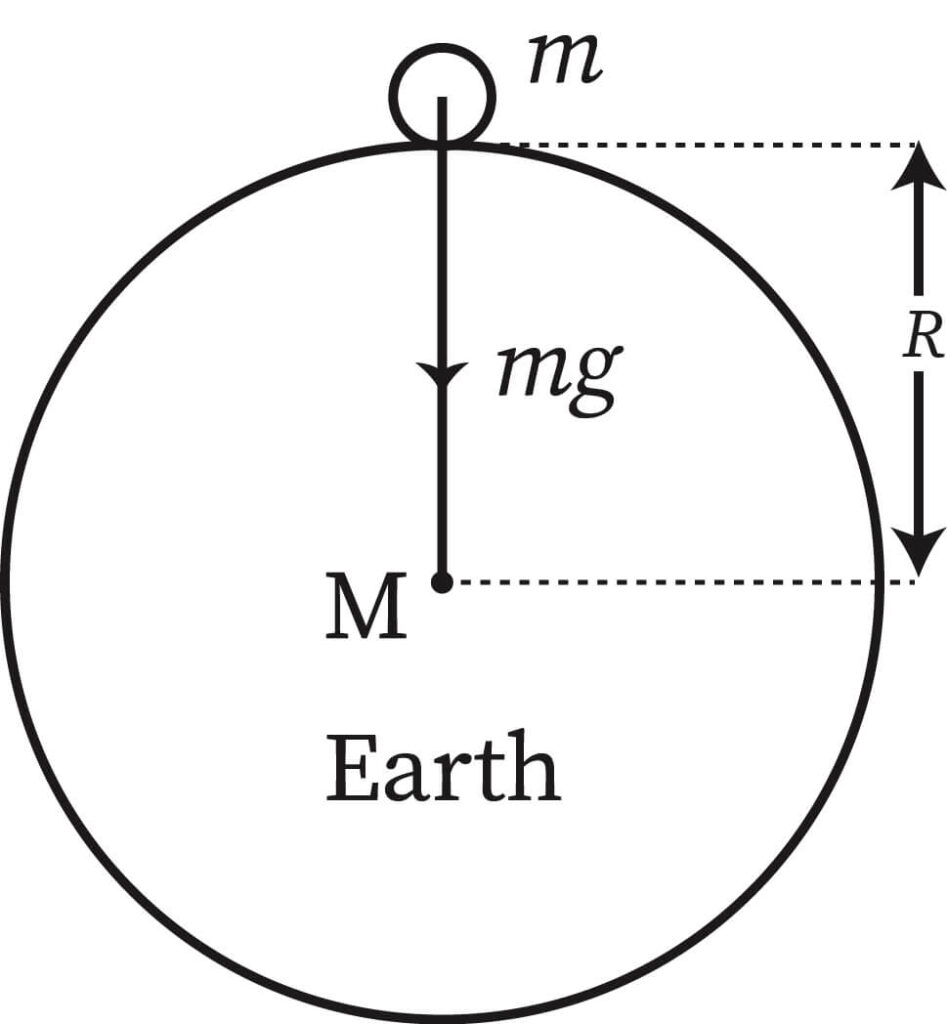
4. For an instance an object falls from a height h above the surface of the earth, considering this height, the formula becomes $\text{F=}\frac{{\text{GM}}_{\text{1}}{\text{M}}_{\text{2}}}{{\left(\text{r+h}\right)}^{\text{2}}}$, but this height is very small and negligible. So the object starts to fall downwards due to gravity with an increase in its velocity when it reaches the earth's surface, the object accelerate and changes the velocity due to the force given by the gravity. the same universal law of gravitation formula becomes So denoting the acceleration due to gravity as 'a', the formula becomes $\text{a=}\frac{{\text{GM}}_{\text{E}}}{{\text{r}}_{\text{E}}{}^{\text{2}}}$where ${\text{M}}_{\text{E}}$ is the mass of the earth and ${\text{r}}_{\text{E}}$ is the radius of the earth.

5. The gravitational acceleration of the body is denoted as "g" and its simplified equation is $\text{g=}\frac{\text{Force}}{\text{mass}}$ of the object. The value of the acceleration due to gravity on earth is $\text{9}{\text{.81m s}}^{\text{-2}}$where the SI unit is ${\text{m/s}}^{\text{2}}$

6. Uniform circular motion and gravity: The first law stated by Newton tells that an object moving at a constant speed will continue to move until and unless there is external force. Let's say an object is moved in a perfect circular motion, a ball tied with a rope and spun in a circular motion continuously, the force that makes it spin in that motion is the centripetal force and this force causes centripetal acceleration. Centripetal means centre seeking. Another common example is the Earth rotating around the sun is also due to centripetal force causing the motion which is due to the gravitational attraction between them. The velocity for an object to travel a distance covered as the circumference of the circular earth and for a time period T is $\text{v=}\frac{\text{2πr}}{\text{T}}$. The centripetal acceleration is $\text{a=}\frac{{\text{v}}^{\text{2}}}{\text{r}}$ where v is the velocity and r is the radius. So the equation of the centripetal force is $\text{F=ma}$ or $\text{F=}\frac{{\text{mv}}^{\text{2}}}{\text{r}}$. The centrifugal force is a force that is created by the inertia of the body and travels in a circular path and acts on the body moving in a circular path which is directed away from the centre around which the body is moving.

Real-life Examples of Acceleration Due to Gravity

1) When a tissue paper and a steel bottle is dropped at the same time, the bottle falls faster than the tissue paper due to the direct proportionality of the mass of the bottle which is higher than the tissue paper

2) Satellites orbiting around the planets and other celestial bodies. The moon and earth are due to the gravitational force.

3) The fruit falls from the tree after it's ripped. Since the mass of the object increases, it falls down. 

NOTE: 

1) The acceleration due to gravity is less of an object that is placed at an height h than the object placed on the surface. 

2) The acceleration due to gravity is more at the poles than at the equator. 

3) There is a difference between free fall motion and falling with air resistance. Free fall motion is when the object falls with the same rate of acceleration irrespective of their mass but when an object falls in the air, it experiences some air resistance due to the surface of the air molecules 

4) The difference between mass and weight is, mass is a quantity of matter in an object which remains constant throughout, whereas weight is a quantity of measure of force exerted on a mass by gravity where it changes according to the gravitational field strength.  

Practice Problem

1) A ball is thrown upward at $\text{30m/s}$ from a plane 500m above the ground.

a) How high does it travel? b) When will it reach its highest point c) When will it reach the ground? 

2) A car has a maximum acceleration of ${\text{6ms}}^{\text{-2}}$. What will its maximum acceleration be while towing the 2nd car of the same mass?

Context and Application 

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for    

• Bachelor of Science Mathematics        
• Master of Science Mathematics