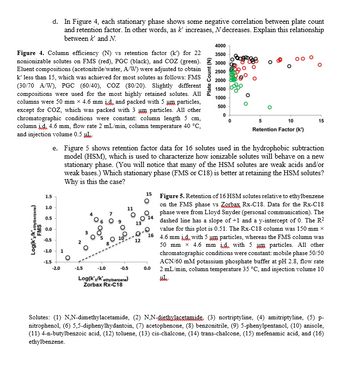
d. In Figure 4, each stationary phase shows some negative correlation between plate count and retention factor. In other words, as k' increases, N decreases. Explain this relationship between k' and N. Plate Count (N) 4000 3500 2500 2000 1500 1000 Figure 4. Column efficiency (N) vs retention factor (k') for 22 nonionizable solutes on FMS (red), PGC (black), and COZ (green). 3000 Eluent compositions (acetonitrile/water, A/W) were adjusted to obtain k' less than 15, which was achieved for most solutes as follows: FMS (30/70 A/W), PGC (60/40), COZ (80/20). Slightly different compositions were used for the most highly retained solutes. All columns were 50 mm × 4.6 mm id and packed with 5 um particles, except for COZ, which was packed with 3 um particles. All other chromatographic conditions were constant: column length 5 cm, column j.§. 4.6 mm, flow rate 2 mL/min, column temperature 40 °C, and injection volume 0.5 μL Log(k'x/K'ethylbenzene) FMS 1.5 1.0 0.5 0.0 ཐྭ ཋ ཤྩ བྷྲ ; 500 0 5 10 Retention Factor (k') 15 e. Figure 5 shows retention factor data for 16 solutes used in the hydrophobic subtraction model (HSM), which is used to characterize how ionizable solutes will behave on a new stationary phase. (You will notice that many of the HSM solutes are weak acids and/or weak bases.) Which stationary phase (FMS or C18) is better at retaining the HSM solutes? Why is this the case? 12 15 Figure 5. Retention of 16 HSM solutes relative to ethylbenzene -0.5 -1.0 1 -1.5 -2.0 -1.5 -1.0 -0.5 0.0 Log(k'x/k'ethylbenzene) Zorbax Rx-C18 14 16 on the FMS phase vs Zorbax Rx-C18. Data for the Rx-C18 phase were from Lloyd Snyder (personal communication). The dashed line has a slope of +1 and a y-intercept of 0. The R² value for this plot is 0.51. The Rx-C18 column was 150 mm × 4.6 mm id with 5 um particles, whereas the FMS column was 50 mm × 4.6 mm id with 5 um particles. All other chromatographic conditions were constant: mobile phase 50/50 ACN/60 mM potassium phosphate buffer at pH 2.8, flow rate 2 mL/min, column temperature 35 °C, and injection volume 10 ut Solutes: (1) N,N-dimethylacetamide, (2) N,N-diethylacetamide. (3) nortriptyline, (4) amitriptyline, (5) p- nitrophenol, (6) 5,5-diphenylhydantoin, (7) acetophenone, (8) benzonitrile, (9) 5-phenylpentanol, (10) anisole, (11) 4-n-butylbenzoic acid, (12) toluene, (13) cis-chalcone, (14) trans-chalcone, (15) mefenamic acid, and (16) ethylbenzene.

What mass of MgCl₂ 6H₂O is required to make a 0.200 dm³ stock solution containing 25.0 ppm Mg(II)? What volumes of this stock solution are required to make 10.0 cm³ standard solutions containing 5.00, 1.00 and 0.10 ppm Mg(II)?

An open tubular column with a diameter of 215 um and a stationary phase thickness on the inner wall of 0.51 um passes unretained solute through in 79 s. A particular solute has a retetion time of 467 s. What is the distribution constant for this solute? Kp = What fraction of time does this solute spend in the stationary phase? ts !! ttotal

4.columns with one million theoretical plates operating by slip flow. The figure shows the gradient separation of two forms of fluorescently labeled bovine serum albumin separated on a)50 x 2.1 mm UHPLC column of 1.7 µm C4 silica particles and b)10 mm x 75µm colloidal crystal column of 470 nm C4 silica nanoparticles. What are the main differences in the chromatogram? What is the reason for the difference? Why does the colloidal crystal column have such a high number of theoretical plates (N)? How is the problem of high pressures with very small particles overcome?

calculate the kovats retention indices for solutes 1 and 2 from the data shown and assume tm=0.50 min (methane)

In a reverse-phase separation, a solute was found to have a retention time of 19.6 min, while an unretained peak had a retention time of 1.45 min when the mobile phase was 20/80 v/v% methanol/water. (b) Calculate the k’ for the solute. (c) Calculate the new k’ if the mobile phase is changed to 60/40 methanol/water assuming identical void volume. (d) Calculate a solvent composition that would bring k’ from initial value to a value of 1.20 using tetrahydrofuran/water mobile phase rather than 20/80 v/v % methanol/water.

A 10-ml transfer pipet and a 200-ml volumetric flask (TC) are used to make 0.100 M and 0.0050 M solutions from a stock solution of 2.000(plus or minus) 0.005 M. Calculate the percent relative error for the three solutions if perfect technique is used. (See Garland Experiments in Physical Chemistry, 10th ed. p. 639-642) Report the two new molaritites

Calculate the vapor pressure of propanol (b.p. 97.0 ∘C97.0 ∘C) at the gas chromatography column temperature of 95.0 ∘C95.0 ∘C using the form of the Clausius–Clapeyron equation shown   ln(?1?2)=−(Δ?vap?)(1?1−1?2)ln(P1P2)=−(ΔHvapR)(1T1−1T2)   where ?R is the ideal gas constant, Δ?vapΔHvap is the enthalpy of vaporization, ?1T1 and ?2T2 are two different temperatures, and ?1P1 and ?2P2 are the vapor pressures at the respective temperatures. The enthalpy of vaporization can be estimated using Trouton's rule, Δ?∘vap=(88 J·mol−1⋅K−1)×?bp.ΔHvap∘=(88 J·mol−1⋅K−1)×Tbp. ?=P=   TorrTorr Calculate the vapor pressure of pentane (b.p. 36.0 ∘C36.0 ∘C) at the same column temperature. ?=P=   TorrTorr For compounds of the same chemical class, what is the relationship between vapor pressure of a compound and retention in gas chromatography? As the vapor pressure decreases, retention time decreases. As the vapor pressure increases, retention time increases. As…

Answer the questions by using the given graph below

A solvent passes through a chromatography column in 3.87 min, but the solute requires 7.60 min. What is the retention factor, k? k = What fraction of the time does the solute spend in the mobile phase in the column? t fraction in mobile phase = The volume of the stationary phase is 0.133 times the volume of the mobile phase in the column (Vs = 0.133VM). What is the distribution constant, Kp, for this system? KD = %3D