1. and for n 2 2, The Fibonacci numbers are defined as follows: fo = 0, fı = 1, and for n > 2, fn = fn-1+ fn-2. Prove that for every positive integer n, f3 + fo + ..+ f3n =(f3n+2 – 1) – 1)
1. and for n 2 2, The Fibonacci numbers are defined as follows: fo = 0, fı = 1, and for n > 2, fn = fn-1+ fn-2. Prove that for every positive integer n, f3 + fo + ..+ f3n =(f3n+2 – 1) – 1)
Elements Of Modern Algebra
8th Edition
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Gilbert, Linda, Jimmie
Chapter3: Groups
Section3.2: Properties Of Group Elements
Problem 30E: 30. Prove statement of Theorem : for all integers .
Related questions
Topic Video
Question
100%
Use Mathematical Induction to prove
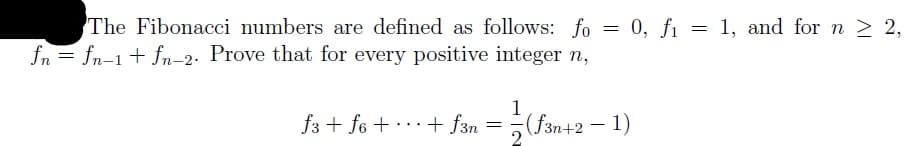
Transcribed Image Text:1. and for n 2 2,
The Fibonacci numbers are defined as follows: fo = 0, fı = 1, and for n > 2,
fn = fn-1+ fn-2. Prove that for every positive integer n,
f3 + fo + ..+ f3n =(f3n+2 – 1)
– 1)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,


Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,


Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning