Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
1. Let z and w be complex numbers. (a) Show that |1+ z w² + |z – w2 = (1+|z|?)(1+ |w/?). (b) Show that z – w? – |z + w|? = -4 Re(z) Re(w). (c) If z and w are in the first or fourth quadrant (but not on the coordinate axes) of the z-plane, < 1. z + w show that 2. Let u(x, y) 2x – x3 + 3xy² for (x, y) E R². Show that u(x, y) is harmonic in C and find an analytic function f(z) = u(T 4) +i v(r u) for z + iu E C Also express f in terms of z

1. Let z and w be complex numbers. (a) Show that |1+ z w² + |z – w2 = (1+|z|?)(1+ |w/?). (b) Show that z – w? – |z + w|? = -4 Re(z) Re(w). (c) If z and w are in the first or fourth quadrant (but not on the coordinate axes) of the z-plane, < 1. z + w show that 2. Let u(x, y) 2x – x3 + 3xy² for (x, y) E R². Show that u(x, y) is harmonic in C and find an analytic function f(z) = u(T 4) +i v(r u) for z + iu E C Also express f in terms of z

Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter8: Applications Of Trigonometry
Section8.6: De Moivre’s Theorem And Nth Roots Of Complex Numbers
Problem 4E
See similar textbooks
icon
Related questions
Question
do first one only
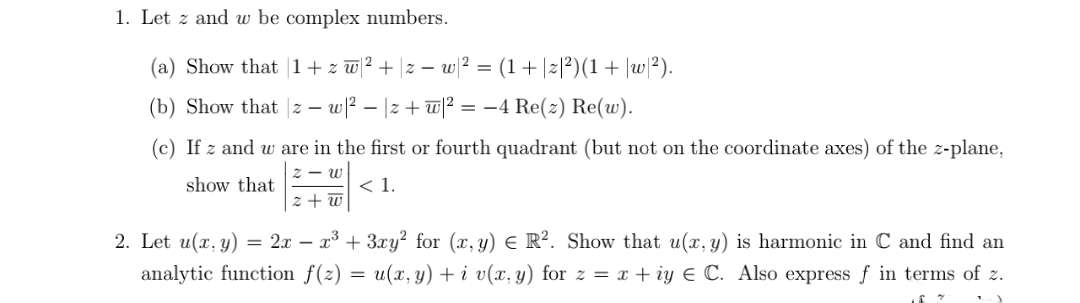
1. Let z and w be complex numbers. (a) Show that 1+ z w 2 + |z – w ? = (1+|z|?)(1+ |w/?). (b) Show that |z – w? – |z + w|2 = –4 Re(z) Re(w). (c) If z and w are in the first or fourth quadrant (but not on the coordinate axes) of the z-plane, 2 - w show that < 1. z + w 2. Let u(x, y) = 2x – x³ + 3xy² for (x, y) E R². Show that u(x, y) is harmonic in C and find an analytic function f(z) = u(x, y) + i v(x, y) for z = x + iy E C. Also express ƒ in terms of z.
Transcribed Image Text:1. Let z and w be complex numbers. (a) Show that 1+ z w 2 + |z – w ? = (1+|z|?)(1+ |w/?). (b) Show that |z – w? – |z + w|2 = –4 Re(z) Re(w). (c) If z and w are in the first or fourth quadrant (but not on the coordinate axes) of the z-plane, 2 - w show that < 1. z + w 2. Let u(x, y) = 2x – x³ + 3xy² for (x, y) E R². Show that u(x, y) is harmonic in C and find an analytic function f(z) = u(x, y) + i v(x, y) for z = x + iy E C. Also express ƒ in terms of z.
Expert Solution
steps

Step by step

Solved in 3 steps with 3 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
Elements Of Modern Algebra
Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,
SEE MORE TEXTBOOKS