1. The monthly revenue R earned by selling x lamps is R(x)= 120x-0.46x The monthly cost of producing x lamps is C(x) 30.25r t 1000. a) How marny lamps must be sold to maximize revenue? What is the maximum revenue? (b) The profit P earned by selling x lamps is given by P(x) R(x)-C(x) How many lamnps must be sold to maximize profit? What is the maximum profit?
1. The monthly revenue R earned by selling x lamps is R(x)= 120x-0.46x The monthly cost of producing x lamps is C(x) 30.25r t 1000. a) How marny lamps must be sold to maximize revenue? What is the maximum revenue? (b) The profit P earned by selling x lamps is given by P(x) R(x)-C(x) How many lamnps must be sold to maximize profit? What is the maximum profit?
Algebra and Trigonometry (MindTap Course List)
4th Edition
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:James Stewart, Lothar Redlin, Saleem Watson
Chapter2: Functions
Section2.4: Average Rate Of Change Of A Function
Problem 4.2E: bThe average rate of change of the linear function f(x)=3x+5 between any two points is ________.
Related questions
Question
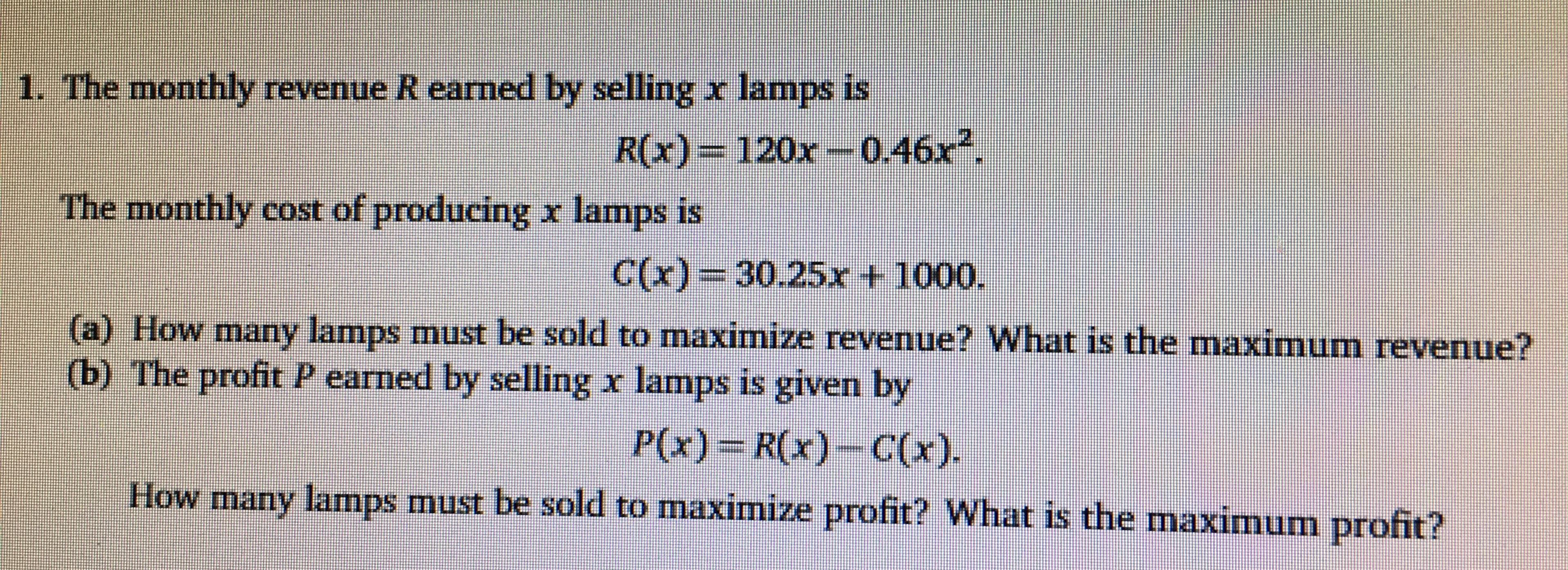
Transcribed Image Text:1. The monthly revenue R earned by selling x lamps is
R(x)= 120x-0.46x
The monthly cost of producing x lamps is
C(x) 30.25r t 1000.
a) How marny lamps must be sold to maximize revenue? What is the maximum revenue?
(b) The profit P earned by selling x lamps is given by
P(x) R(x)-C(x)
How many lamnps must be sold to maximize profit? What is the maximum profit?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning