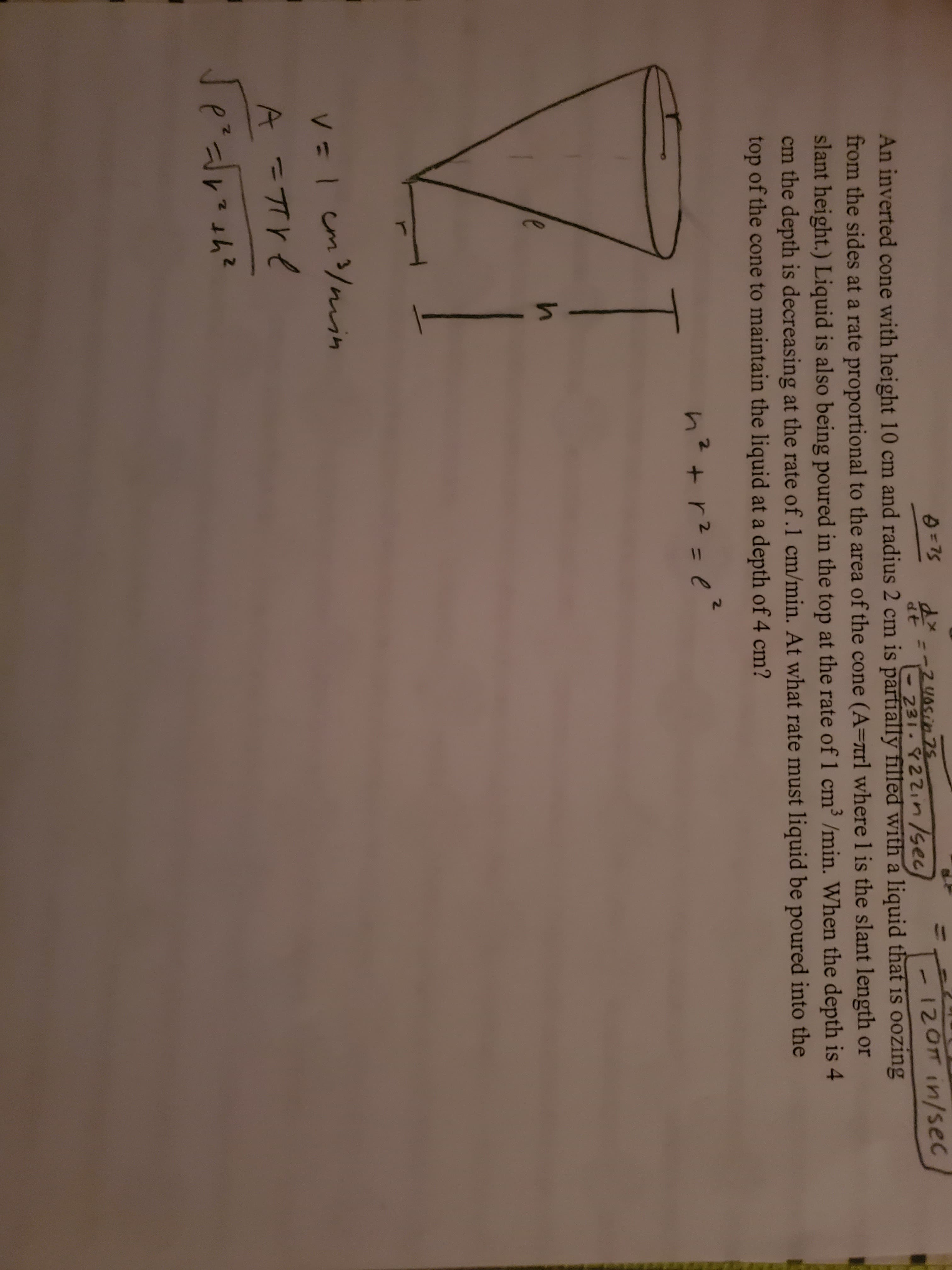
231-22in/sec 12OTIN/sec An inverted cone with height 10 cm and radius 2 cm is partially filled with a liquid that is oozing from the sides at a rate proportional to the area of the cone (A=7trl where l is the slant length or slant height.) Liquid is also being poured in the top at the rate of 1 cm3 /min. When the depth is 4 the depth is decreasing at the rate of .1 cm/min. At what ratemust liquid be poured into the top of the cone to maintain the liquid at a depth of 4 cm? e =1cm/nuih A -TTY Z2 e 2
231-22in/sec 12OTIN/sec An inverted cone with height 10 cm and radius 2 cm is partially filled with a liquid that is oozing from the sides at a rate proportional to the area of the cone (A=7trl where l is the slant length or slant height.) Liquid is also being poured in the top at the rate of 1 cm3 /min. When the depth is 4 the depth is decreasing at the rate of .1 cm/min. At what ratemust liquid be poured into the top of the cone to maintain the liquid at a depth of 4 cm? e =1cm/nuih A -TTY Z2 e 2
Chapter3: Functions
Section3.3: Rates Of Change And Behavior Of Graphs
Problem 45SE: A driver of a car stopped at a gas station to fill up his gas tank. He looked at his watch, and the...
Related questions
Question
Transcribed Image Text:231-22in/sec
12OTIN/sec
An inverted cone with height 10 cm and radius 2 cm is partially filled with a liquid that is oozing
from the sides at a rate proportional to the area of the cone (A=7trl where l is the slant length or
slant height.) Liquid is also being poured in the top at the rate of 1 cm3 /min. When the depth is 4
the depth is decreasing at the rate of .1 cm/min. At what ratemust liquid be poured into the
top of the cone to maintain the liquid at a depth of 4 cm?
e
=1cm/nuih
A -TTY
Z2
e
2
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

