6. Let A be an n x n hermitian matrix, i.e. A = A*. Assume that all n eigenvalues are different. Then the normalized eigenvectors { v; : j = 1,...,n} form an orthonormal basis in C". Consider В %3 (Ах — их, Ах - их) %3D (Ах — их)"(Ах — vх) | where (,) denotes the scalar product in C" and u,v are real constants with µ < v. Show that if no eigenvalue lies between µ and v, then B > 0.
6. Let A be an n x n hermitian matrix, i.e. A = A*. Assume that all n eigenvalues are different. Then the normalized eigenvectors { v; : j = 1,...,n} form an orthonormal basis in C". Consider В %3 (Ах — их, Ах - их) %3D (Ах — их)"(Ах — vх) | where (,) denotes the scalar product in C" and u,v are real constants with µ < v. Show that if no eigenvalue lies between µ and v, then B > 0.
Linear Algebra: A Modern Introduction
4th Edition
ISBN:9781285463247
Author:David Poole
Publisher:David Poole
Chapter7: Distance And Approximation
Section7.1: Inner Product Spaces
Problem 11AEXP
Related questions
Question
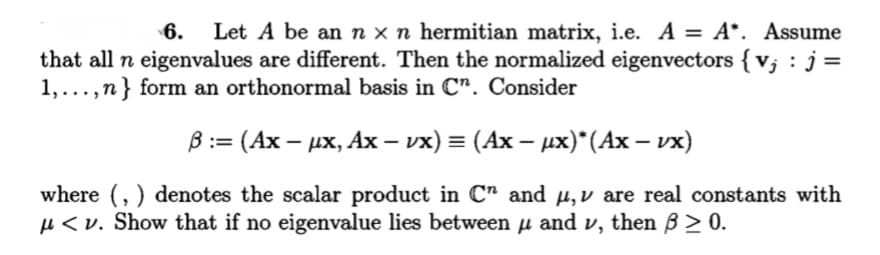
Transcribed Image Text:6.
Let A be an n x n hermitian matrix, i.e. A = A*. Assume
that all n eigenvalues are different. Then the normalized eigenvectors { v; : j =
1,...,n} form an orthonormal basis in C". Consider
B:= (Ax – ux, Ax – vx) = (Ax – ux)*(Ax – vx)
|
where (, ) denotes the scalar product in C" and µ,v are real constants with
µ < v. Show that if no eigenvalue lies between µ and v, then B > 0.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning