Could you explain how to show 7.30 in detail? I also included lists of definitions and theorems in the book as a reference. Theorem 7.11 (Cauchy's Theorem). Let G be a finite group, and suppose that aprime p divides its order. Then G has an element of order p.Corollary 7.3. Let p be a prime. Then a finite group G is a p-group if and only if|G| = p", for some n > 0.Corollary 7.4. Let p be a prime and G a finite group. Then G has just one Sylowp-subgroup if and only if the Sylow p-subgroup is normal in G.Theorem 7.12. Let G be a group of order pq, where p and q are primes with p < q.Then the Sylow q-subgroup of G is normal. In particular, G is not simple.Example 7.11. Let us show that there are no simple groups of order 351. As 351 =33. 13, we note that the number of Sylow 3-subgroups is 1 + 3k and divides 13 andthe number of Sylow 13-subgroups is 1+ 131 and divides 27, with k, l e Z. Theonly solutions for l are 0 and 2; that is, the number of Sylow 13-subgroups is either1 or 27. If it is 1, then we know that the Sylow 13-subgroup is normal, and we aredone. So let us assume that it is 27. Now, each Sylow 13-subgroup is of order 13.In a group of prime order, everything but the identity has order equal to that of thegroup; thus, each Sylow 13-subgroup has 12 elements of order 13. Furthermore, if Pand Q are different Sylow 13-subgroups, then since |P N Q| must divide |P| = 13,either P = Q (which is impossible) or P n Q = {e}. Thus, each of the 27 Sylow13-subgroups contributes 12 elements of order 13, and there is no overlap. We havenow used up 12 · 27 = 324 elements of the group. This leaves only 351 – 324 = 27elements. But that is the size of one Sylow 3-subgroup! Thus, there is only roomfor one such subgroup. In order words, either the Sylow 13-subgroup or the Sylow3-subgroup must be normal.-Theorem 7.13. Let G be a group of order pqr, where p, q and r are distinct primes.Then G is not simple.Theorem 7.14. Let G be a group of order p... p"*, where the p; are distinctprimes and the n¡ are positive integers. If, for each i, G has a unique SylowPi-subgroup P;, then G = P¡ x ..× Pk.Example 7.12. Suppose we wish to classify the groups of order 45. The number ofSylow 3-subgroups is 1+ 3k and divides 5, for some k e Z. Thus, it can only be 1.The number of Sylow 5-subgroups is 1+51 and divides 9, for some l e Z. Therefore,the Sylow 5-subgroup is unique as well. According to the preceding theorem, a groupof order 45 must be the direct product of its Sylow subgroups. By Corollary 7.2, aof order 9 is isomorphic to either Z3 x Z3 or Z,, and Corollary 4.2 tells us thata group of order 5 is isomorphic to Z5. 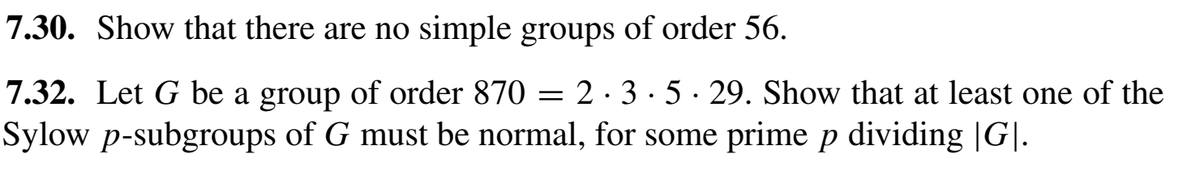Hence, every group of order 45 is isomorphicto either Z3 x Z3 × Z5 or Z9 × Z5 (and these are not isomorphic to each other, byTheorem 5.6).group 7.30. Show that there are no simple groups of order 56.2·3·5· 29. Show that at least one of the7.32. Let G be a group of order 870Sylow p-subgroups of G must be normal, for some prime p dividing |G|.

Answered: Image /qna-images/answer/0b8313a3-173d-4152-9ef7-970cdb7d6bc2.jpg

Answered: 7.30. Show that there are no simple…

Math

Advanced Math

7.30. Show that there are no simple groups of order 56.

Elements Of Modern Algebra

8th Edition

ISBN:9781285463230

Author:Gilbert, Linda, Jimmie

Publisher:Gilbert, Linda, Jimmie

Chapter4: More On Groups

Section4.8: Some Results On Finite Abelian Groups (optional)

Problem 6E: 6. For each of the following values of , describe all the abelian groups of order , up to...

See similar textbooks

Similar questions

6. For each of the following values of , describe all the abelian groups of order , up to isomorphism. b. c. d. e. f.
Exercises 13. For each of the following values of, find all subgroups of the group described in Exercise, addition and state their order. a. b. c. d. e. f.
Suppose G1 and G2 are groups with normal subgroups H1 and H2, respectively, and with G1/H1 isomorphic to G2/H2. Determine the possible orders of H1 and H2 under the following conditions. a. G1=24 and G2=18 b. G1=32 and G2=40
Let G be the group and H the subgroup given in each of the following exercises of Section 4.4. In each case, is H normal in G? Exercise 3 b. Exercise 4 c. Exercise 5 d. Exercise 6 e. Exercise 7 f. Exercise 8 Section 4.4 Let H be the subgroup e, of the octic group D4. Find the distinct left cosets of H in D4, write out their elements, partition D4 into left cosets of H, and give [D4:H]. Find the distinct right cosets of H in D4, write out their elements, and partition D4 into right cosets of H. Let H be the subgroup e, of the octic group D4. Find the distinct left cosets of H in D4, write out their elements, partition D4 into left cosets of H, and give [D4:H]. Find the distinct right cosets of H in D4, write out their elements, and partition D4 into right cosets of H. Let H be the subgroup e, of the octic group D4. Find the distinct left cosets of H in D4, write out their elements, partition D4 into left cosets of H, and give [D4:H]. Find the distinct right cosets of H in D4, write out their elements, and partition D4 into right cosets of H. Let H be the subgroup (1),(2,3) of S3. Find the distinct left cosets of H in S3, write out their elements, partition S3 into left cosets of H, and give [S3:H]. Find the distinct right cosets of H in S3, write out their elements, and partition S3 into right cosets of H. In Exercises 7 and 8, let G be the multiplicative group of permutation matrices I3,P3,P32,P1,P4,P2 in Example 6 of Section 3.5 Let H be the subgroup of G given by H=I3,P4={ (100010001),(001010100) }. Find the distinct left cosets of H in G, write out their elements, partition G into left cosets of H, and give [G:H]. Find the distinct right cosets of H in G, write out their elements, and partition G into right cosets of H. Let H be the subgroup of G given by H=I3,P3,P32={ (100010001),(010001100),(001100010) }. Find the distinct left cosets of H in G, write out their elements, partition G into left cosets of H, and give [G:H]. Find the distinct right cosets of H in G, write out their elements, and partition G into right cosets of H.
Exercises 31. Let be a group with its center: . Prove that if is the only element of order in , then .
Show that An has index 2 in Sn, and thereby conclude that An is always a normal subgroup of Sn.
Find the normalizer of the subgroup (1),(1,3)(2,4) of the octic group D4.
15. Assume that can be written as the direct sum , where is a cyclic group of order . Prove that has elements of order but no elements of order greater than Find the number of distinct elements of that have order .
Suppose that the abelian group G can be written as the direct sum G=C22C3C3, where Cn is a cyclic group of order n. Prove that G has elements of order 12 but no element of order greater than 12. Find the number of distinct elements of G that have order 12.
1. Consider , the groups of units in under multiplication. For each of the following subgroups in , partition into left cosets of , and state the index of in a. b.
Exercises 10. For each of the following values of, find all subgroups of the cyclic group under addition and state their order. a. b. c. d. e. f.
Let H and K be subgroups of a group G and K a subgroup of H. If the order of G is 24 and the order of K is 3, what are all the possible orders of H?