A box with a square base and open top must have a volume of 500 cm³. We wish to find the dimensions of the box that minimize the amount of material used. First, find a formula for the surface area of the box in terms of only x, the length of one side of the square base. Simplify your formula as much as possible. A(x) = Next, find the derivative, A'(x). A'(x) = Now, calculate when the derivative equals zero, that is, when A'(x): 0. A'(x) = 0 when x = We next have to make sure that this value of x gives a minimum value for the surface area. Let's use the second derivative test. Find A"(x). = (x).V Evaluate A"(x) at the x-value you gave above.
A box with a square base and open top must have a volume of 500 cm³. We wish to find the dimensions of the box that minimize the amount of material used. First, find a formula for the surface area of the box in terms of only x, the length of one side of the square base. Simplify your formula as much as possible. A(x) = Next, find the derivative, A'(x). A'(x) = Now, calculate when the derivative equals zero, that is, when A'(x): 0. A'(x) = 0 when x = We next have to make sure that this value of x gives a minimum value for the surface area. Let's use the second derivative test. Find A"(x). = (x).V Evaluate A"(x) at the x-value you gave above.
Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)
6th Edition
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Bruce Crauder, Benny Evans, Alan Noell
Chapter2: Graphical And Tabular Analysis
Section2.1: Tables And Trends
Problem 1TU: If a coffee filter is dropped, its velocity after t seconds is given by v(t)=4(10.0003t) feet per...
Related questions
Question
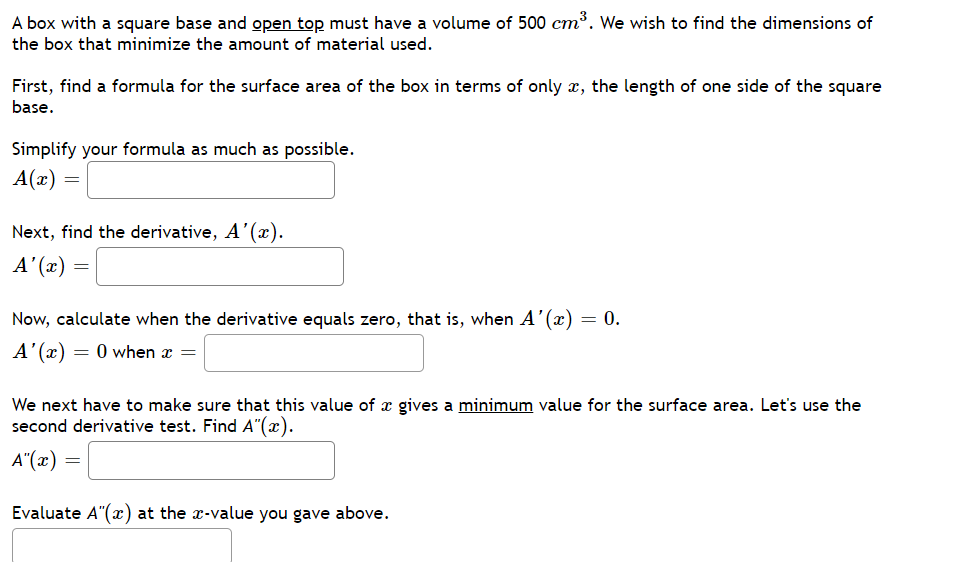
Transcribed Image Text:A box with a square base and open top must have a volume of 500 cm³. We wish to find the dimensions of
the box that minimize the amount of material used.
First, find a formula for the surface area of the box in terms of only x, the length of one side of the square
base.
Simplify your formula as much as possible.
A(x)
Next, find the derivative, A'(x).
A'(x) =
Now, calculate when the derivative equals zero, that is, when A'(x) = 0.
A'(x) = 0 when x =
We next have to make sure that this value of x gives a minimum value for the surface area. Let's use the
second derivative test. Find A"(x).
A"(x) =
Evaluate A"(x) at the x-value you gave above.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning