Homework Help is Here – Start Your Trial Now!
Math
Calculus
A house painter has found that the number of jobs that he has each year is decreasing with respect to the number of years he has been in business. The number of jobs he has each year can be modeled j(x) = 104.55 jobs X where x is the number of years since 2004. The painter has kept records of the average amount he was paid for each job. His income per job is presented in the table. Average Income per Job Income (dollars) Year 2004 430 2005 559 2006 727 2007 945 2008 1228 2009 1597 2010 2075 (a) Find an exponential model for average income per job, p, with input x aligned to years since 2004. (Remember to paste the unrounded function model into your calculator before reporting the answer with all numerical values rounded to three decimal places.) p(x) 430.07(1.300)* dollars per job gives the average amount the painter was paid per job x years after 2004, 0 s x s 6 (b) The equation for the painter's annual income is tx) = j(x)p(x) dollars. (c) What was the painter's income in 2010? (Remember to avoid intermediate rounding.) Round your answer to two decimal places. 36171.96 How rapidly was the painter's income changing in 2010? (Round your answer to two decimal places.) $237.73 Xper year

A house painter has found that the number of jobs that he has each year is decreasing with respect to the number of years he has been in business. The number of jobs he has each year can be modeled j(x) = 104.55 jobs X where x is the number of years since 2004. The painter has kept records of the average amount he was paid for each job. His income per job is presented in the table. Average Income per Job Income (dollars) Year 2004 430 2005 559 2006 727 2007 945 2008 1228 2009 1597 2010 2075 (a) Find an exponential model for average income per job, p, with input x aligned to years since 2004. (Remember to paste the unrounded function model into your calculator before reporting the answer with all numerical values rounded to three decimal places.) p(x) 430.07(1.300)* dollars per job gives the average amount the painter was paid per job x years after 2004, 0 s x s 6 (b) The equation for the painter's annual income is tx) = j(x)p(x) dollars. (c) What was the painter's income in 2010? (Remember to avoid intermediate rounding.) Round your answer to two decimal places. 36171.96 How rapidly was the painter's income changing in 2010? (Round your answer to two decimal places.) $237.73 Xper year

Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
18th Edition
ISBN:9780079039897
Author:Carter
Publisher:Carter
Chapter8: Polynomials
Section8.1: Adding And Subtracting Polynomials
Problem 44PPS
See similar textbooks
icon
Related questions
Question
100%
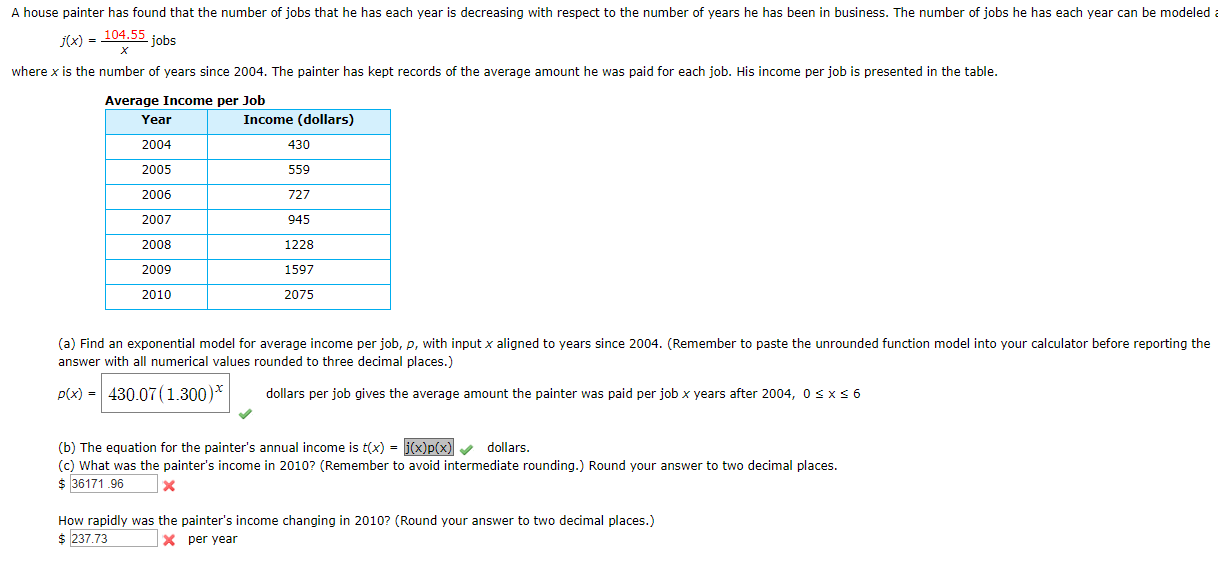
A house painter has found that the number of jobs that he has each year is decreasing with respect to the number of years he has been in business. The number of jobs he has each year can be modeled j(x) = 104.55 jobs X where x is the number of years since 2004. The painter has kept records of the average amount he was paid for each job. His income per job is presented in the table. Average Income per Job Income (dollars) Year 2004 430 2005 559 2006 727 2007 945 2008 1228 2009 1597 2010 2075 (a) Find an exponential model for average income per job, p, with input x aligned to years since 2004. (Remember to paste the unrounded function model into your calculator before reporting the answer with all numerical values rounded to three decimal places.) p(x) 430.07(1.300)* dollars per job gives the average amount the painter was paid per job x years after 2004, 0 s x s 6 (b) The equation for the painter's annual income is tx) = j(x)p(x) dollars. (c) What was the painter's income in 2010? (Remember to avoid intermediate rounding.) Round your answer to two decimal places. 36171.96 How rapidly was the painter's income changing in 2010? (Round your answer to two decimal places.) $237.73 Xper year
Transcribed Image Text:A house painter has found that the number of jobs that he has each year is decreasing with respect to the number of years he has been in business. The number of jobs he has each year can be modeled j(x) = 104.55 jobs X where x is the number of years since 2004. The painter has kept records of the average amount he was paid for each job. His income per job is presented in the table. Average Income per Job Income (dollars) Year 2004 430 2005 559 2006 727 2007 945 2008 1228 2009 1597 2010 2075 (a) Find an exponential model for average income per job, p, with input x aligned to years since 2004. (Remember to paste the unrounded function model into your calculator before reporting the answer with all numerical values rounded to three decimal places.) p(x) 430.07(1.300)* dollars per job gives the average amount the painter was paid per job x years after 2004, 0 s x s 6 (b) The equation for the painter's annual income is tx) = j(x)p(x) dollars. (c) What was the painter's income in 2010? (Remember to avoid intermediate rounding.) Round your answer to two decimal places. 36171.96 How rapidly was the painter's income changing in 2010? (Round your answer to two decimal places.) $237.73 Xper year
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 4 steps with 4 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897…
Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill
Algebra: Structure And Method, Book 1
Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell
Big Ideas Math A Bridge To Success Algebra 1: Stu…
Big Ideas Math A Bridge To Success Algebra 1: Stu…
Algebra
ISBN:
9781680331141
Author:
HOUGHTON MIFFLIN HARCOURT
Publisher:
Houghton Mifflin Harcourt
College Algebra
College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition…
Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
SEE MORE TEXTBOOKS