A pair of parametric equations is given. 3 cos(t), y 4 sin(t), 0 sts 2T x (a) Sketch the curve represented by the parametric equations. Use arrows to indicate the direction of the curve as t increases у У 2 2 х X 2 -2- -2 у 2 X х -4 -2 2 -4 -2 2 4 -2 (b) Find a rectangular-coordinate equation for the curve by eliminating the parameter.
A pair of parametric equations is given. 3 cos(t), y 4 sin(t), 0 sts 2T x (a) Sketch the curve represented by the parametric equations. Use arrows to indicate the direction of the curve as t increases у У 2 2 х X 2 -2- -2 у 2 X х -4 -2 2 -4 -2 2 4 -2 (b) Find a rectangular-coordinate equation for the curve by eliminating the parameter.
Algebra and Trigonometry (MindTap Course List)
4th Edition
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:James Stewart, Lothar Redlin, Saleem Watson
Chapter8: Polar Coordinates And Parametric Equations
Section8.FOM: Focus On Modeling: The Path Of A Projectile
Problem 6P: Shooting into the Wind Suppose that a projectile is fired into a headwind that pushes it back so as...
Related questions
Question
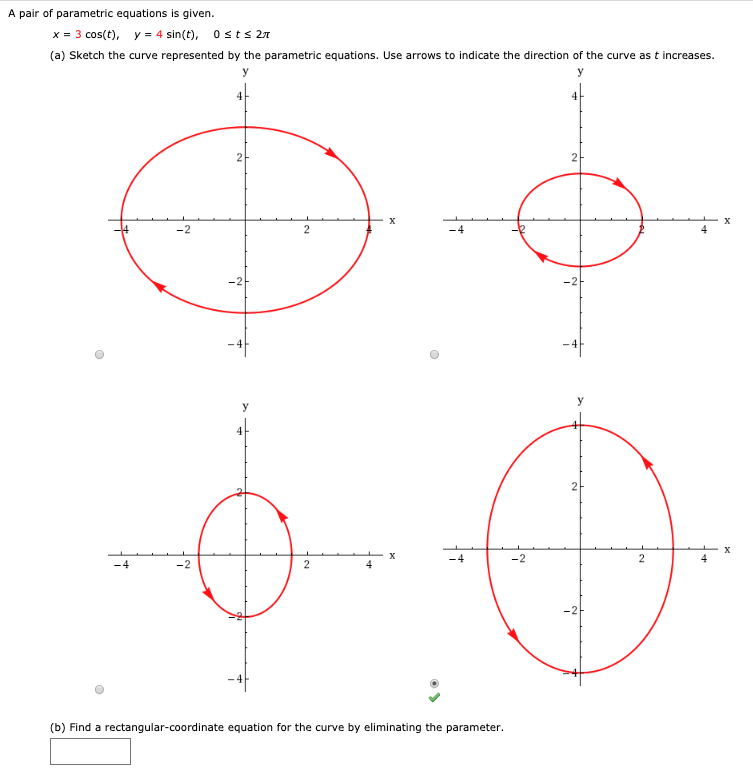
Transcribed Image Text:A pair of parametric equations is given.
3 cos(t), y
4 sin(t), 0 sts 2T
x
(a) Sketch the curve represented by the parametric equations. Use arrows to indicate the direction of the curve as t increases
у
У
2
2
х
X
2
-2-
-2
у
2
X
х
-4
-2
2
-4
-2
2
4
-2
(b) Find a rectangular-coordinate equation for the curve by eliminating the parameter.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning