Combine the product and quotient rules with polynomials Question f@}g[#) If f(5) = 3, f' (5) = -4, g(5) h(z) =-6, g'(5)-9, h(5) -5, and h' (5) = -3 what is k (5)? Let k(æ) = Do not include "k' (5) =" in your answer. For example, if you found k (5) 7, you would enter 7 = Provide your answer below: SUBMIT FEEDBACK MORE INSTRUCTION
Combine the product and quotient rules with polynomials Question f@}g[#) If f(5) = 3, f' (5) = -4, g(5) h(z) =-6, g'(5)-9, h(5) -5, and h' (5) = -3 what is k (5)? Let k(æ) = Do not include "k' (5) =" in your answer. For example, if you found k (5) 7, you would enter 7 = Provide your answer below: SUBMIT FEEDBACK MORE INSTRUCTION
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter4: Polynomial And Rational Functions
Section4.3: Zeros Of Polynomials
Problem 3E
Related questions
Question
100%
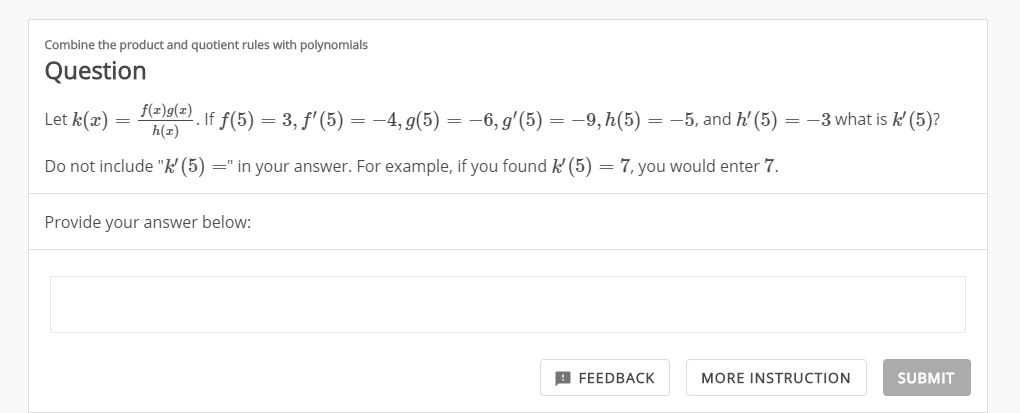
Transcribed Image Text:Combine the product and quotient rules with polynomials
Question
f@}g[#) If f(5) = 3, f' (5) = -4, g(5)
h(z)
=-6, g'(5)-9, h(5)
-5, and h' (5) = -3 what is k (5)?
Let k(æ)
=
Do not include "k' (5) =" in your answer. For example, if you found k (5)
7, you would enter 7
=
Provide your answer below:
SUBMIT
FEEDBACK
MORE INSTRUCTION
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage