Consider the DE which is linear with constant coefficients. d²y dx² First we will work on solving the corresponding homogeneous equation. The auxiliary equation (using m as your variable) is = 0 which has root Because this is a repeated root, we don't have much choice but to use the exponential function corresponding to this root: 3/2 dy 8 + 16y = x dx reduction of order. Y2 = ue4x Then (using the prime notation for the derivatives) = y₁ = So, plugging y2 into the left side of the differential equation, and reducing, we get y8y2 + 16y2 = U= So now our equation is exu" =x. To solve for u we need only integrate xe twice, using a as our first constant of integration and b as the second we get -4x Therefore y2 = general solution. to do the We knew from the beginning that e4 was a solution. We have worked out is that xe4 is another solution to the homogeneous equation, which is generally the case 2+4x when we have multiple roots. Then 24 is the particular 64 solution to the nonhomogeneous equation, and the general solution we derived is pieced together using superposition.
Consider the DE which is linear with constant coefficients. d²y dx² First we will work on solving the corresponding homogeneous equation. The auxiliary equation (using m as your variable) is = 0 which has root Because this is a repeated root, we don't have much choice but to use the exponential function corresponding to this root: 3/2 dy 8 + 16y = x dx reduction of order. Y2 = ue4x Then (using the prime notation for the derivatives) = y₁ = So, plugging y2 into the left side of the differential equation, and reducing, we get y8y2 + 16y2 = U= So now our equation is exu" =x. To solve for u we need only integrate xe twice, using a as our first constant of integration and b as the second we get -4x Therefore y2 = general solution. to do the We knew from the beginning that e4 was a solution. We have worked out is that xe4 is another solution to the homogeneous equation, which is generally the case 2+4x when we have multiple roots. Then 24 is the particular 64 solution to the nonhomogeneous equation, and the general solution we derived is pieced together using superposition.
Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
18th Edition
ISBN:9780079039897
Author:Carter
Publisher:Carter
Chapter7: Exponents And Exponential Functions
Section7.8: Transforming Exponential Expressions
Problem 13PFA
Related questions
Question
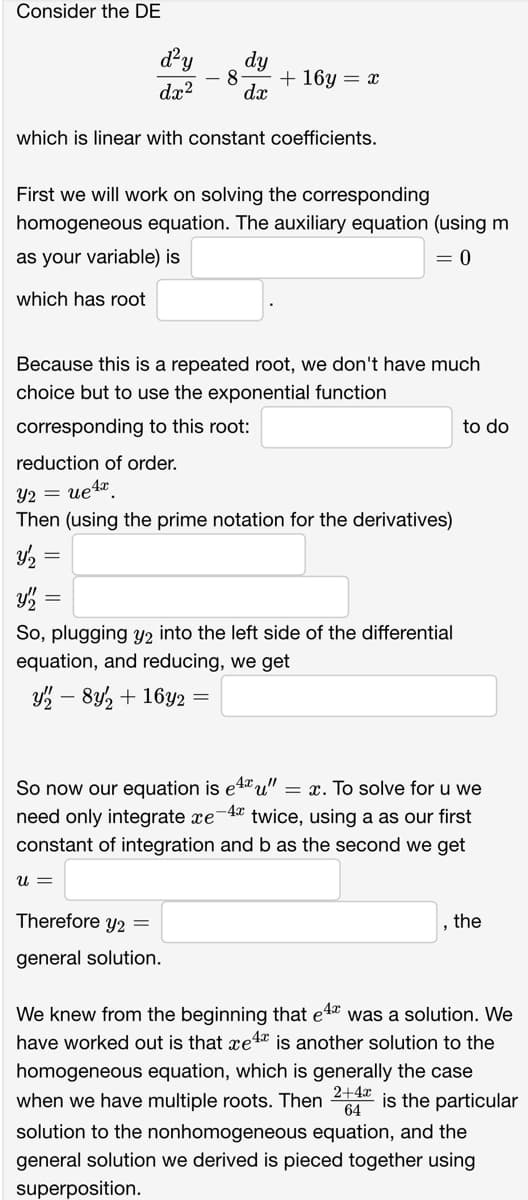
Transcribed Image Text:Consider the DE
d²y dy
dx²
which is linear with constant coefficients.
8 + 16y = x
dx
First we will work on solving the corresponding
homogeneous equation. The auxiliary equation (using m
as your variable) is
= 0
which has root
Because this is a repeated root, we don't have much
choice but to use the exponential function
corresponding to this root:
reduction of order.
Y2 =
ue4x
Then (using the prime notation for the derivatives)
Y/₂
Y
So, plugging y2 into the left side of the differential
equation, and reducing, we get
y2-8y2 + 16y2 =
U =
So now our equation is e4u" = x. To solve for u we
need only integrate ce-4 twice, using a as our first
constant of integration and b as the second we get
Therefore y2 =
general solution.
to do
the
We knew from the beginning that e4 was a solution. We
have worked out is that xe4 is another solution to the
homogeneous equation, which is generally the case
when we have multiple roots. Then 2+4 is the particular
64
solution to the nonhomogeneous equation, and the
general solution we derived is pieced together using
superposition.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 4 steps

Recommended textbooks for you

Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage


Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
