Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
Consider the following proposed proof of the triangle inequality (different from the proof in the textbook). Let x and y be arbitrary real numbers. The conclusion is trivial when |x + y = 0, so suppose that |x + y > 0. 1. (x + y)² = x² + 2x|ly| + y² by algebra and Proposition 1.3.1(iv). 2. x² + 2xy + y² ≥ x² + 2xy + y² = (x + y)² by Proposition 1.3.1 parts (iii) and (vi); and algebra. 3. Combining the previous two steps with Proposition 1.3.1(iv) shows that (x + y)² ≥ |x + y ². 4. The contrapositive of Proposition 1.1.8(vi) then implies the desired conclusion that |x + y ≥ x + y). Select the option that best describes this proposed proof. Step 4 is faulty. Step 3 is faulty. Step 2 is faulty. The proof is valid. Step 1 is faulty.

Consider the following proposed proof of the triangle inequality (different from the proof in the textbook). Let x and y be arbitrary real numbers. The conclusion is trivial when |x + y = 0, so suppose that |x + y > 0. 1. (x + y)² = x² + 2x|ly| + y² by algebra and Proposition 1.3.1(iv). 2. x² + 2xy + y² ≥ x² + 2xy + y² = (x + y)² by Proposition 1.3.1 parts (iii) and (vi); and algebra. 3. Combining the previous two steps with Proposition 1.3.1(iv) shows that (x + y)² ≥ |x + y ². 4. The contrapositive of Proposition 1.1.8(vi) then implies the desired conclusion that |x + y ≥ x + y). Select the option that best describes this proposed proof. Step 4 is faulty. Step 3 is faulty. Step 2 is faulty. The proof is valid. Step 1 is faulty.

Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter10: Sequences, Series, And Probability
Section: Chapter Questions
Problem 63RE
See similar textbooks
icon
Related questions
Question

Please work out with explaination

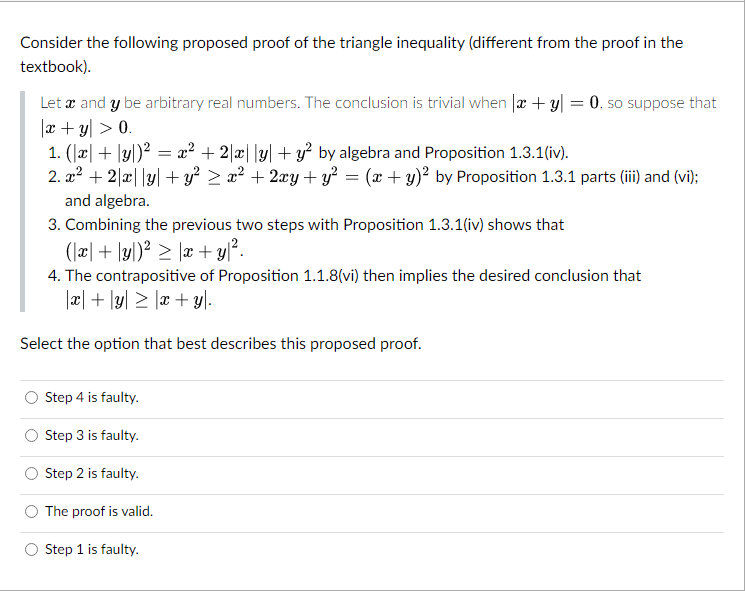
Consider the following proposed proof of the triangle inequality (different from the proof in the textbook). Let x and y be arbitrary real numbers. The conclusion is trivial when |x + y = 0, so suppose that |x + y > 0. 1. (x + y)² = x² + 2x|ly| + y² by algebra and Proposition 1.3.1(iv). 2. x² + 2xy + y² ≥ x² + 2xy + y² = (x + y)² by Proposition 1.3.1 parts (iii) and (vi); and algebra. 3. Combining the previous two steps with Proposition 1.3.1(iv) shows that (x + y)² ≥ |x + y ². 4. The contrapositive of Proposition 1.1.8(vi) then implies the desired conclusion that |x + y ≥ x + y). Select the option that best describes this proposed proof. Step 4 is faulty. Step 3 is faulty. Step 2 is faulty. The proof is valid. Step 1 is faulty.
Transcribed Image Text:Consider the following proposed proof of the triangle inequality (different from the proof in the textbook). Let x and y be arbitrary real numbers. The conclusion is trivial when |x + y = 0, so suppose that |x + y > 0. 1. (x + y)² = x² + 2x|ly| + y² by algebra and Proposition 1.3.1(iv). 2. x² + 2xy + y² ≥ x² + 2xy + y² = (x + y)² by Proposition 1.3.1 parts (iii) and (vi); and algebra. 3. Combining the previous two steps with Proposition 1.3.1(iv) shows that (x + y)² ≥ |x + y ². 4. The contrapositive of Proposition 1.1.8(vi) then implies the desired conclusion that |x + y ≥ x + y). Select the option that best describes this proposed proof. Step 4 is faulty. Step 3 is faulty. Step 2 is faulty. The proof is valid. Step 1 is faulty.
Expert Solution
steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
Linear Algebra: A Modern Introduction
Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning
Elements Of Modern Algebra
Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,
SEE MORE TEXTBOOKS