Determine the points on a function when tangent lines have a given slope Question 16x3 - 4x2 6x - 13 have a tangent line of slope 5? For which value(s) of x does f(x) = 3 If there is more than one answer, give all of the x-values separated by commas, e.g. if f (x) has a tangent line of slope 5 at x = 3 and x = 5 enter 3, 5.
Determine the points on a function when tangent lines have a given slope Question 16x3 - 4x2 6x - 13 have a tangent line of slope 5? For which value(s) of x does f(x) = 3 If there is more than one answer, give all of the x-values separated by commas, e.g. if f (x) has a tangent line of slope 5 at x = 3 and x = 5 enter 3, 5.
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter4: Polynomial And Rational Functions
Section4.5: Rational Functions
Problem 51E
Related questions
Question
100%
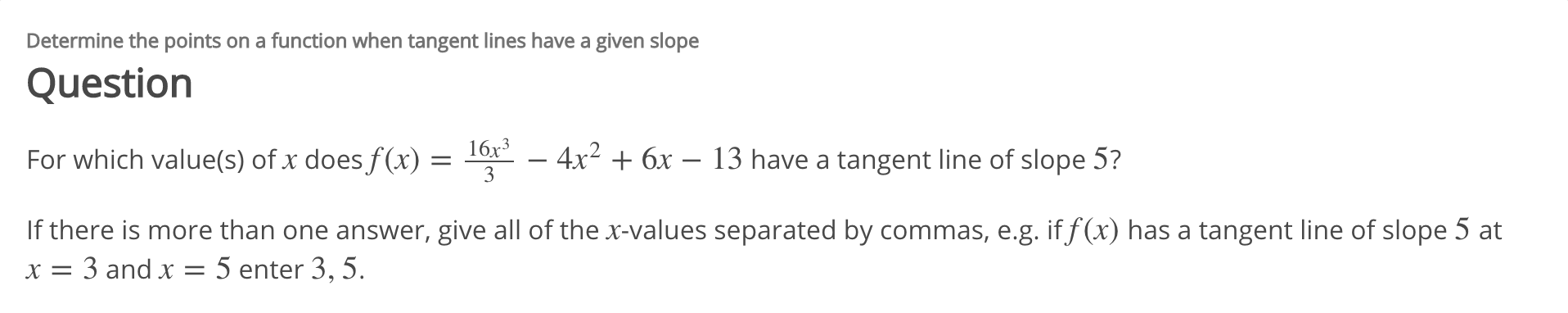
Transcribed Image Text:Determine the points on a function when tangent lines have a given slope
Question
16x3
- 4x2 6x - 13 have a tangent line of slope 5?
For which value(s) of x does f(x) =
3
If there is more than one answer, give all of the x-values separated by commas, e.g. if f (x) has a tangent line of slope 5 at
x = 3 and x = 5 enter 3, 5.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning