E R?, z is the optimal value for each linear relaxation, and (x1, x2) is a corresponding solution. F Z= a, え= 16, x,-3.9 X <3 2 = az X;=6.2, 2,=3 2,= 5, x2=4 と;56 , >7
E R?, z is the optimal value for each linear relaxation, and (x1, x2) is a corresponding solution. F Z= a, え= 16, x,-3.9 X <3 2 = az X;=6.2, 2,=3 2,= 5, x2=4 と;56 , >7
Computer Networking: A Top-Down Approach (7th Edition)
7th Edition
ISBN:9780133594140
Author:James Kurose, Keith Ross
Publisher:James Kurose, Keith Ross
Chapter1: Computer Networks And The Internet
Section: Chapter Questions
Problem R1RQ: What is the difference between a host and an end system? List several different types of end...
Related questions
Question
After several iterations of the branch and bound
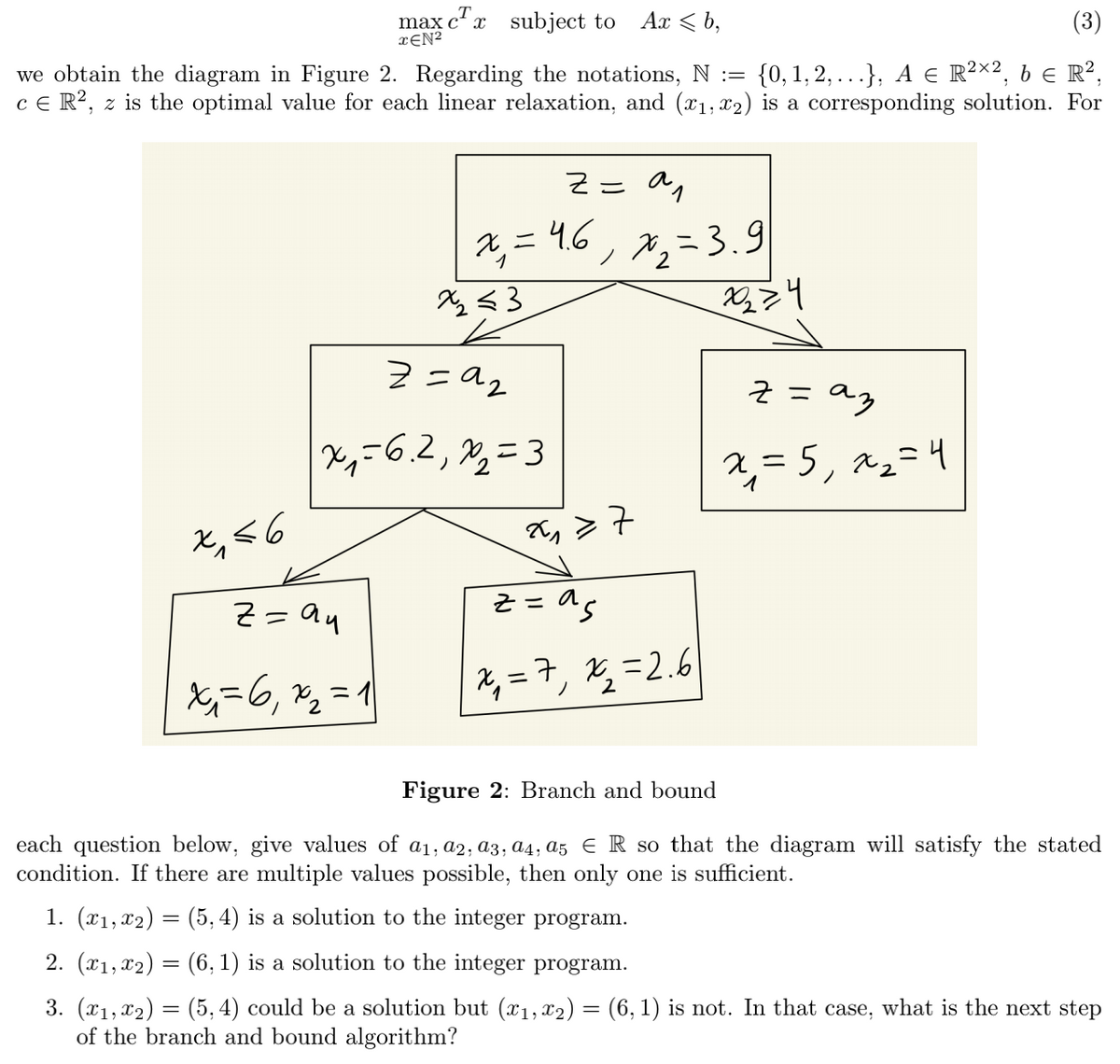
Transcribed Image Text:max c' x subject to Ax < b,
xƐN?
(3)
we obtain the diagram in Figure 2. Regarding the notations, N := {0,1, 2, ...}, A E R²×2, b e R²,
ce R?, z is the optimal value for each linear relaxation, and (x1, x2) is a corresponding solution. For
Z= a,
2, = 46, x,=3.9
= 3.9
ニ
2く3
Z = ag
X,=6.2, 2,=3
2, = 5, x2=4
と,<6
X, > 7
z = as
X=6, %2 = 1
2, = 7, X, =2.6
ノ
Figure 2: Branch and bound
each question below, give values of a1, a2, a3, a4; a5 E R so that the diagram will satisfy the stated
condition. If there are multiple values possible, then only one is sufficient.
1. (x1, x2) = (5, 4) is a solution to the integer program.
2. (x1, x2) = (6, 1) is a solution to the integer program.
3. (x1, x2) = (5,4) could be a solution but (x1, x2) = (6, 1) is not. In that case, what is the next step
of the branch and bound algorithm?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps

Recommended textbooks for you

Computer Networking: A Top-Down Approach (7th Edi…
Computer Engineering
ISBN:
9780133594140
Author:
James Kurose, Keith Ross
Publisher:
PEARSON

Computer Organization and Design MIPS Edition, Fi…
Computer Engineering
ISBN:
9780124077263
Author:
David A. Patterson, John L. Hennessy
Publisher:
Elsevier Science

Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:
9781337569330
Author:
Jill West, Tamara Dean, Jean Andrews
Publisher:
Cengage Learning

Computer Networking: A Top-Down Approach (7th Edi…
Computer Engineering
ISBN:
9780133594140
Author:
James Kurose, Keith Ross
Publisher:
PEARSON

Computer Organization and Design MIPS Edition, Fi…
Computer Engineering
ISBN:
9780124077263
Author:
David A. Patterson, John L. Hennessy
Publisher:
Elsevier Science

Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:
9781337569330
Author:
Jill West, Tamara Dean, Jean Andrews
Publisher:
Cengage Learning

Concepts of Database Management
Computer Engineering
ISBN:
9781337093422
Author:
Joy L. Starks, Philip J. Pratt, Mary Z. Last
Publisher:
Cengage Learning

Prelude to Programming
Computer Engineering
ISBN:
9780133750423
Author:
VENIT, Stewart
Publisher:
Pearson Education

Sc Business Data Communications and Networking, T…
Computer Engineering
ISBN:
9781119368830
Author:
FITZGERALD
Publisher:
WILEY