F, г х F,
A:
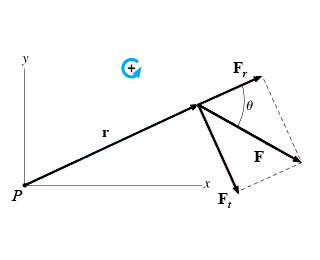
Moment arm of the force
In the figure, the dashed line extending from the force
What is rm, the length of the moment arm of the force F about point P?
Express your answer in terms of r and θ.
Find the moment M about P due to F. Your answer should correctly express both the magnitude and the sign of M.
Express your answer in terms of either rm and F or r, θ, and F.
B:
As shown (Figure 2), resolve the force vector, F, into radial (parallel to r) and tangential (perpendicular to r) components. Find the magnitude of the radial and tangential components, Fr and Ft. Assume that θis between zero and 90 degrees.
Express your answers in terms of F and θ
Is the following statement true or false?
The moment about point P is proportional to the length r of the position vector, r.
|
true |
|
false |
Is the following statement true or false?
Both the radial and tangential components of F generate moments about point P.
|
true |
|
false |
Is the following statement true or false?
In this problem, the tangential force vector would tend to rotate an object clockwise around pivot point P.
|
true |
|
false |
Find the moment M about the pivot point P due to the force F. Your answer should correctly express both the magnitude and sign of M.
Express your answer in terms of either Fr and r or F, θ, and r.

Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 6 images


