Finalising a Mail Merge will, dynamically update the letter for each recipient dynamically update the letter for all recipients create an individual letter for each selected recipient
Finalising a Mail Merge will, dynamically update the letter for each recipient dynamically update the letter for all recipients create an individual letter for each selected recipient
Database Systems: Design, Implementation, & Management
12th Edition
ISBN:9781305627482
Author:Carlos Coronel, Steven Morris
Publisher:Carlos Coronel, Steven Morris
Chapter11: Database Performance Tuning And Query Optimization
Section: Chapter Questions
Problem 21P: Problems 1721 are based on the following query: SELECT V_CODE, V_NAME, V_CONTACT, V_STATE FROM...
Related questions
Question
100%
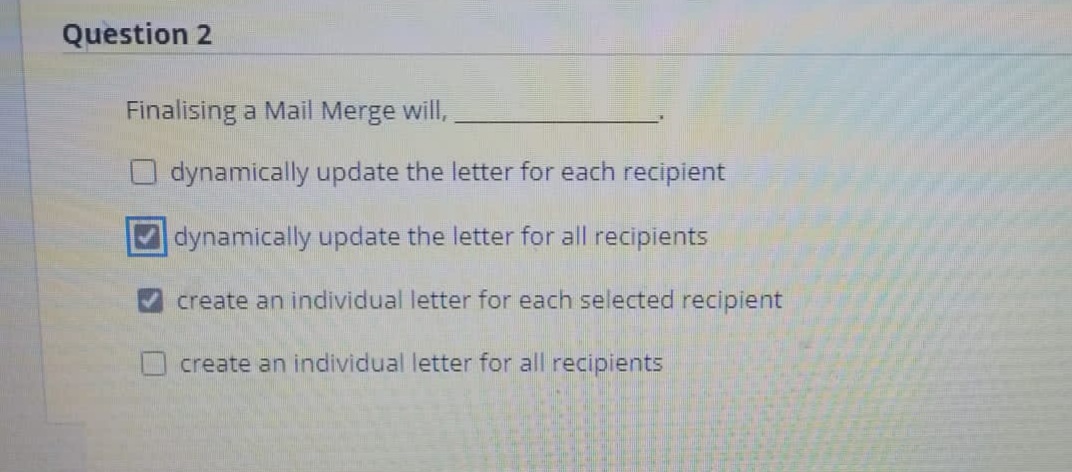
Transcribed Image Text:Question 2
Finalising a Mail Merge will,
dynamically update the letter for each recipient
dynamically update the letter for all recipients
create an individual letter for each selected recipient
create an individual letter for all recipients
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Recommended textbooks for you

Database Systems: Design, Implementation, & Manag…
Computer Science
ISBN:
9781305627482
Author:
Carlos Coronel, Steven Morris
Publisher:
Cengage Learning

Database Systems: Design, Implementation, & Manag…
Computer Science
ISBN:
9781285196145
Author:
Steven, Steven Morris, Carlos Coronel, Carlos, Coronel, Carlos; Morris, Carlos Coronel and Steven Morris, Carlos Coronel; Steven Morris, Steven Morris; Carlos Coronel
Publisher:
Cengage Learning

Database Systems: Design, Implementation, & Manag…
Computer Science
ISBN:
9781305627482
Author:
Carlos Coronel, Steven Morris
Publisher:
Cengage Learning

Database Systems: Design, Implementation, & Manag…
Computer Science
ISBN:
9781285196145
Author:
Steven, Steven Morris, Carlos Coronel, Carlos, Coronel, Carlos; Morris, Carlos Coronel and Steven Morris, Carlos Coronel; Steven Morris, Steven Morris; Carlos Coronel
Publisher:
Cengage Learning