Find the equation of the tangent line to the following curve at the indicated point. 36 at (1,- 6) xy2 у - Click if you would like to Show Work for this question: Open Show Work SHOW HINT LINK TO TEXT By accessing this Question Assistance, you will learn while you earn points based on the Point Potential Policy set by your 3.7 3.7 Study I 2000-2019 John Wiley & Sons, Inc. All Rights Reserved. A Division of John Wiley & Sons Inc. I Privacy Policy
Find the equation of the tangent line to the following curve at the indicated point. 36 at (1,- 6) xy2 у - Click if you would like to Show Work for this question: Open Show Work SHOW HINT LINK TO TEXT By accessing this Question Assistance, you will learn while you earn points based on the Point Potential Policy set by your 3.7 3.7 Study I 2000-2019 John Wiley & Sons, Inc. All Rights Reserved. A Division of John Wiley & Sons Inc. I Privacy Policy
Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)
6th Edition
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Bruce Crauder, Benny Evans, Alan Noell
Chapter1: Functions
Section1.2: Functions Given By Tables
Problem 32SBE: Does a Limiting Value Occur? A rocket ship is flying away from Earth at a constant velocity, and it...
Related questions
Question
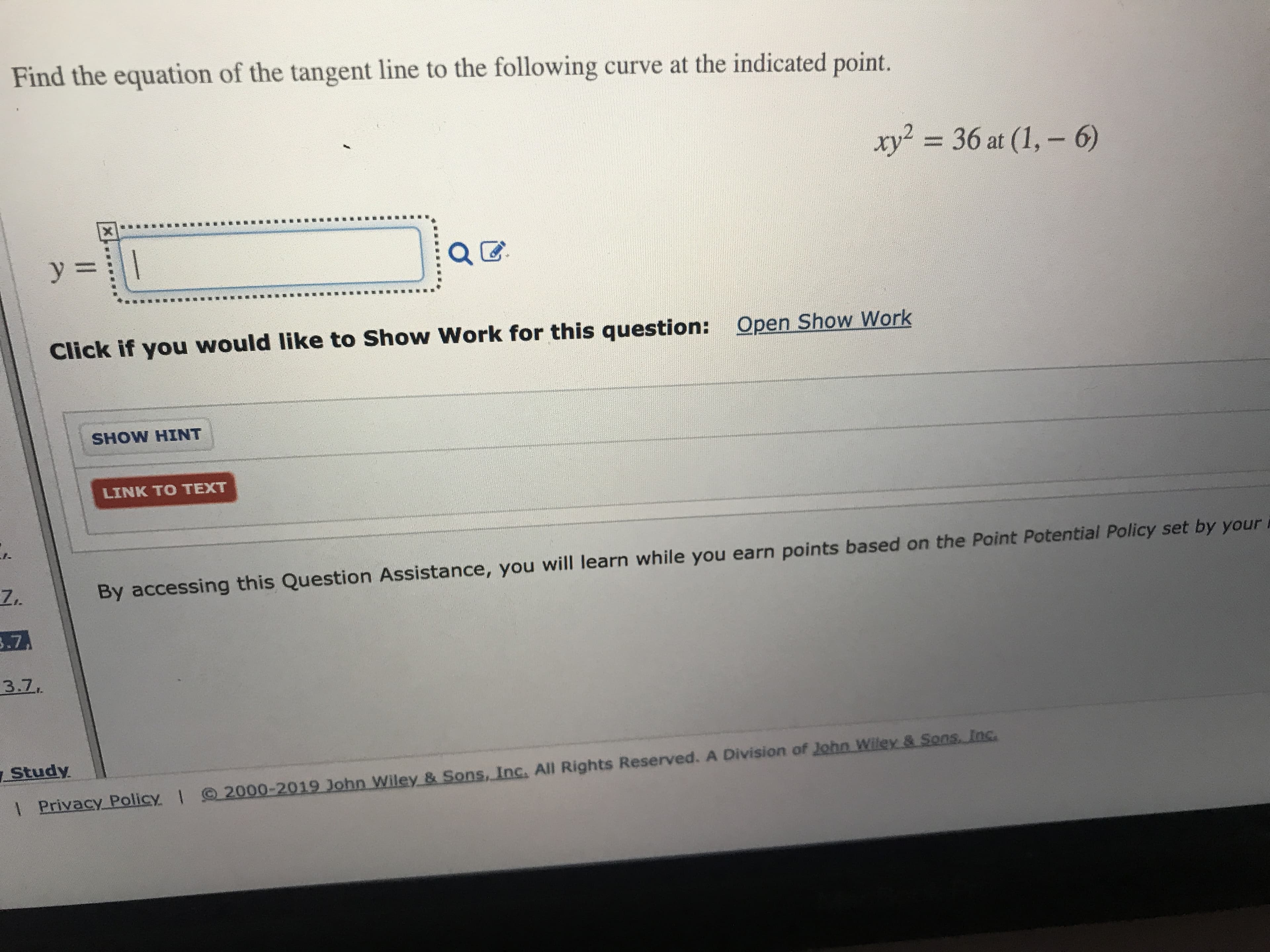
Transcribed Image Text:Find the equation of the tangent line to the following curve at the indicated point.
36 at (1,- 6)
xy2
у -
Click if you would like to Show Work for this question:
Open Show Work
SHOW HINT
LINK TO TEXT
By accessing this Question Assistance, you will learn while you earn points based on the Point Potential Policy set by your
3.7
3.7
Study
I 2000-2019 John Wiley & Sons, Inc. All Rights Reserved. A Division of John Wiley & Sons Inc.
I Privacy Policy
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning