Find the following using a technique discussed in Section 8.4. 162 mod 45 = 164 mod 45 = 168 mod 45 = 1616 mod 45% = Need Help? Watch It Read It
Find the following using a technique discussed in Section 8.4. 162 mod 45 = 164 mod 45 = 168 mod 45 = 1616 mod 45% = Need Help? Watch It Read It
Elements Of Modern Algebra
8th Edition
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Gilbert, Linda, Jimmie
Chapter2: The Integers
Section2.5: Congruence Of Integers
Problem 57E
Related questions
Question
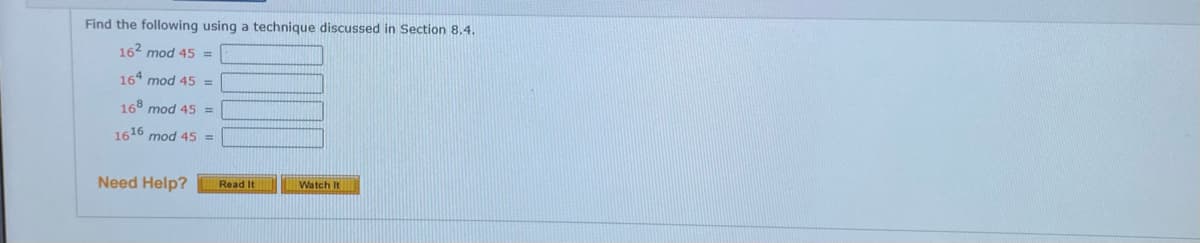
Transcribed Image Text:Find the following using a technique discussed in Section 8.4.
162 mod 45 =
164 mod 45 =
168 mod 45 =
1616 mod 45 =
Need Help?
Watch It
Read It

Transcribed Image Text:Example 8.4.4
Computing a mod n When k Is a Power of 2
Find 144 mod 713.
Solution Use property (8.4.1) to write 144 = (1442)?. Then
1444 mod 713 = (1442)² mod 713
= (1442 mod 713)? mod 713
= (20736 mod 713) mod 713
because 1442 = 20736
= 592 mod 713
because 20736 mod 713 = 59
= 3481 mod 713
because 592 = 3481
= 629
because 3481 mod 713 = 629.
Example 8.4.5
Computing a" mod n When k Is Not a Power of 2
Find 123 mod 713.
anon
2 Jeds
Solution First write the exponent as a sum of powers of 2:
43 = 2° + 23 + 2+1 = 32+8+2+1.
Next compute 12 for k = 0, 1, 2, 3, 4, and 5.
12 mod 713 = 12
122 mod 713 = 144
12 mod 713 = 144?mod 713 = 59
by Example 8.4.4
128 mod 713 = 592 mod 713
= 629 by Example 8.4.4
1216 mod 713 = 6292 mod T713 = 639 by the method of Example 8.4.4
1232 mod 713 = 6392 mod 713 = 485 by the method of Example 8.4.4.
By property (8.4.2),
1243 = 1232+8 +2+1 = 1232.128. 12²- 12'.
Thus, by Corollary 8.4.4,
1243 mod 713
= {(1232 mod 713)·(12° mod 713)·(122 mod 713)·(12 mod 713)} mod 713.
By substitution,
1245 mod 713 = (485·629·144·12) mod 713
= 527152320 mod 713
= 48.
You should know how to do the computations in Example 8.4.5 by hand using only a
simple electronic calculator, but if you are computing a lot of residues, especially ones
involving large numbers, you may want to write a short computer or calculator program to
do the computations for you.
Extending the Euclidean Algorithm
An extended version of the Euclidean algorithm can be used to find a concrete expression
for the greatest common divisor of integers a and b.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,