Trigonometry (MindTap Course List)
10th Edition
ISBN:9781337278461
Author:Ron Larson
Publisher:Ron Larson
Chapter6: Topics In Analytic Geometry
Section6.2: Introduction To Conics: parabolas
Problem 4ECP: Find an equation of the tangent line to the parabola y=3x2 at the point 1,3.
Related questions
Question
100%
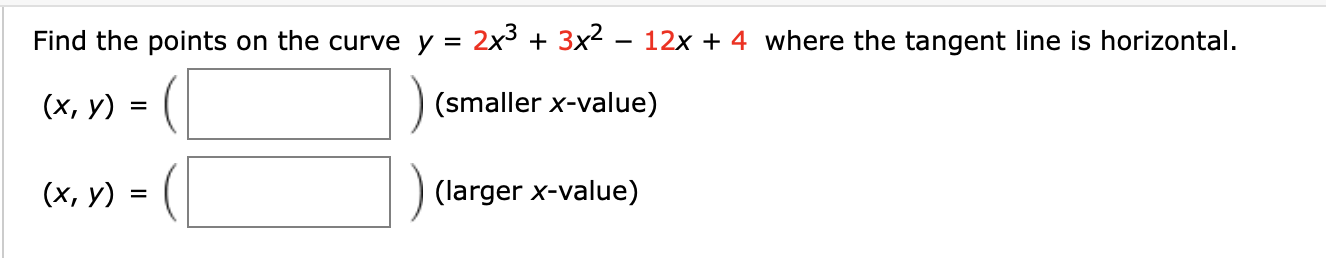
Transcribed Image Text:Find the points on the curve y = 2x3
3x2 - 12x
4 where the tangent line is horizontal.
(х, у)
(smaller x-value)
(х, у) з
(larger x-value)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning