Consider a feedback-based causal LTI system with input x(t) shown in Figure 6.41, where G(s) is the transfer function of a "loop filter" and 1/s is an integrator. The idea is to use the error e(t) to drive these, so as to make y(t) track x(t). (a) Find the transfer functions H(s) = X(s) and He(s): E(s) = X(s)* (b) Now set G(s) = 10. This is termed "proportional feedback," where the feedback is propor- tional to the error. (i) Find y(t) and e(t) for x(t) = sin 10t. (ii) How do your answers change (provide a qualitative discussion) for x(t): sin 100t? = sint and x(t): (iii) For x(t) = u(t) (unit step), find and sketch y(t) and e(t), and specify their asymptotic values as t∞. (iv) For x(t) = tu(t) (ramp starting at time zero), find the asymptotic value of the error e(t) as t → ∞. Hint: You can simply use the final value theorem in (iii). (c) Redo (b)(iv) for G(s) = 10+½½ ("proportional plus integral" feedback).
Consider a feedback-based causal LTI system with input x(t) shown in Figure 6.41, where G(s) is the transfer function of a "loop filter" and 1/s is an integrator. The idea is to use the error e(t) to drive these, so as to make y(t) track x(t). (a) Find the transfer functions H(s) = X(s) and He(s): E(s) = X(s)* (b) Now set G(s) = 10. This is termed "proportional feedback," where the feedback is propor- tional to the error. (i) Find y(t) and e(t) for x(t) = sin 10t. (ii) How do your answers change (provide a qualitative discussion) for x(t): sin 100t? = sint and x(t): (iii) For x(t) = u(t) (unit step), find and sketch y(t) and e(t), and specify their asymptotic values as t∞. (iv) For x(t) = tu(t) (ramp starting at time zero), find the asymptotic value of the error e(t) as t → ∞. Hint: You can simply use the final value theorem in (iii). (c) Redo (b)(iv) for G(s) = 10+½½ ("proportional plus integral" feedback).
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
Related questions
Question
please have step by step solution and explain. thank you very much
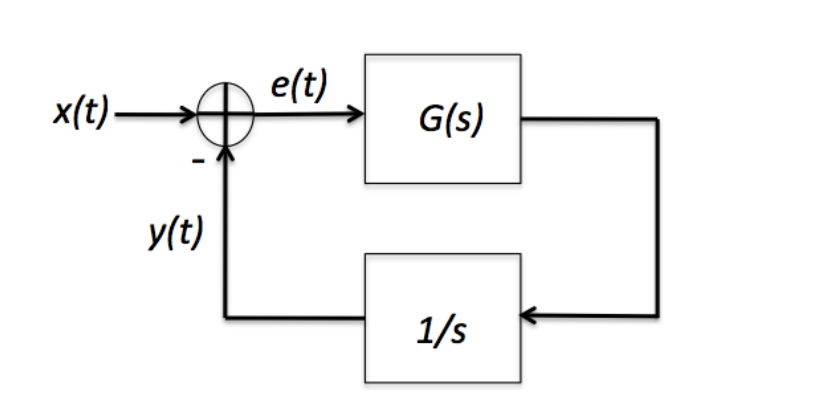
Transcribed Image Text:x(t) —
e(t)
G(s)
y(t)
1/s

Transcribed Image Text:Consider a feedback-based causal LTI system with input x(t) shown in Figure
6.41, where G(s) is the transfer function of a "loop filter" and 1/s is an integrator. The idea is
to use the error e(t) to drive these, so as to make y(t) track x(t).
(a) Find the transfer functions H(s) =
Y(s)
X(s)
and He(s)
=
E(s)
X(s)*
(b) Now set G(s) = 10. This is termed "proportional feedback,” where the feedback is propor-
tional to the error.
(i) Find y(t) and e(t) for x(t) = sin 10t.
(ii) How do your answers change (provide a qualitative discussion) for x(t) = sint and x(t) =
sin 100t?
=
(iii) For x(t) = u(t) (unit step), find and sketch y(t) and e(t), and specify their asymptotic values
as t∞.
(iv) For x(t) = tu(t) (ramp starting at time zero), find the asymptotic value of the error e(t) as
t → ∞.
Hint: You can simply use the final value theorem in (iii).
(c) Redo (b)(iv) for G(s) = 10 + ½ (“proportional plus integral" feedback).
S
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Step 1: Summarize the given information.
VIEWStep 2: Determine transfer functions.
VIEWStep 3: Determine outputs for x(t) = sin(100t).
VIEWStep 4: Determine outputs for x(t) = sin(100t).
VIEWStep 5: Determine output for step input, x(t) = u(t).
VIEWStep 6: Find asymptotic error for ramp input, x(t) = tu(t).
VIEWStep 7: Find asymptotic error for proportional plus integral feedback.
VIEWSolution
VIEWTrending now
This is a popular solution!
Step by step
Solved in 8 steps with 39 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
for your answer for part b ii what happened to x(j10)? sin10t should be equal to =10/s^2+100, since its the laplace transform. i need more explaination on the y(t) answer too. how did the angle become sin? i am so confused on your answer

Transcribed Image Text:Consider a feedback-based causal LTI system with input x(t) shown in Figure
6.41, where G(s) is the transfer function of a "loop filter" and 1/s is an integrator. The idea is
to use the error e(t) to drive these, so as to make y(t) track x(t).
(a) Find the transfer functions H(s) =
Y(s)
X(s)
and He(s) =
=
E(s)
X(s)*
(b) Now set G(s) = 10. This is termed “proportional feedback," where the feedback is propor-
tional to the error.
(i) Find y(t) and e(t) for x(t)
sin 10t.
(ii) How do your answers change (provide a qualitative discussion) for x(t)
sin 100t?
=
sint and x(t)
(iii) For x(t) = u(t) (unit step), find and sketch y(t) and e(t), and specify their asymptotic values
as t∞.
(iv) For x(t) = tu(t) (ramp starting at time zero), find the asymptotic value of the error e(t) as
t → ∞.
Hint: You can simply use the final value theorem in (iii).
(c) Redo (b)(iv) for G(s) = 10+ 2/3 ("proportional plus integral" feedback).
![The input signal is given by,
x(t)=sin(10t).
Its angular frequency is w = 10 rad/s.
The corresponding output and error signals in frequency domain are
Y(j10)=H(10) X(10)
1
=
Z-tan
1(100) × 1
×120°,
102+100
=
·Z-45°;
√2
E(j10) = H¸(j10)·X(j10)
1
√10²+100
1
= - 45°.
√2
In time-domain,
[90°-tan-1 (100)] × 120°,
1
y(t)=
sin(10t―45º),
√2
e(t) =
sin(10t+45°).
√2](https://content.bartleby.com/qna-images/question/1d86b7f3-5570-4ce2-ade5-b05f7393fda1/cb501521-05c2-44d9-940a-daa68163e395/nspa4m_thumbnail.png)
Transcribed Image Text:The input signal is given by,
x(t)=sin(10t).
Its angular frequency is w = 10 rad/s.
The corresponding output and error signals in frequency domain are
Y(j10)=H(10) X(10)
1
=
Z-tan
1(100) × 1
×120°,
102+100
=
·Z-45°;
√2
E(j10) = H¸(j10)·X(j10)
1
√10²+100
1
= - 45°.
√2
In time-domain,
[90°-tan-1 (100)] × 120°,
1
y(t)=
sin(10t―45º),
√2
e(t) =
sin(10t+45°).
√2
Solution
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education

Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education

Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON

Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,