f(t) dt, where f is the function whose graph is shown below. You can assume the graph off is symmetric across the y-axis. Let g(x) (a) Evaluate g(-3) and g(3) g(-3) g(3) (b) Estimate g(-2), g(-1), and g(0) to the nearest half-unit. g(-2) g(-1) g(0) (c) Determine the x-interval on which g is increasing. Ifg is never increasing, type "N" in each blank x-interval < x< (d) Where does g have its maximum value? х%3 Graph of f: 1 1 0
f(t) dt, where f is the function whose graph is shown below. You can assume the graph off is symmetric across the y-axis. Let g(x) (a) Evaluate g(-3) and g(3) g(-3) g(3) (b) Estimate g(-2), g(-1), and g(0) to the nearest half-unit. g(-2) g(-1) g(0) (c) Determine the x-interval on which g is increasing. Ifg is never increasing, type "N" in each blank x-interval < x< (d) Where does g have its maximum value? х%3 Graph of f: 1 1 0
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter4: Polynomial And Rational Functions
Section: Chapter Questions
Problem 15T
Related questions
Question
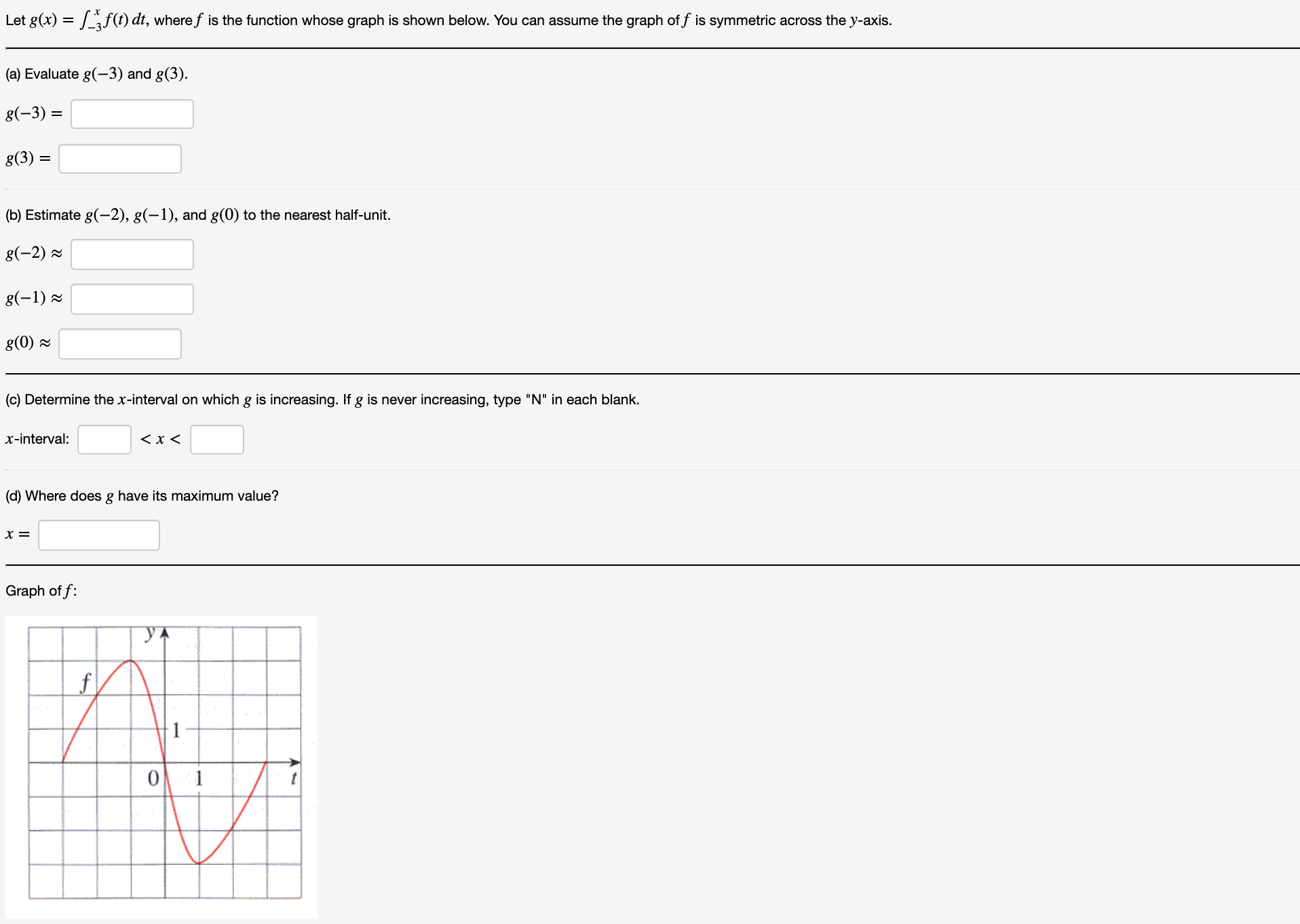
Transcribed Image Text:f(t) dt, where f is the function whose graph is shown below. You can assume the graph off is symmetric across the y-axis.
Let g(x)
(a) Evaluate g(-3) and g(3)
g(-3)
g(3)
(b) Estimate g(-2), g(-1), and g(0) to the nearest half-unit.
g(-2)
g(-1)
g(0)
(c) Determine the x-interval on which g is increasing. Ifg is never increasing, type "N" in each blank
x-interval
< x<
(d) Where does g have its maximum value?
х%3
Graph of f:
1
1
0
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning