Giveň á šéčónd órder linéär hómögenéðuš différêntial équatión a2(x)y" +a1(x)y' + ao(x)y=0 we know that a fundamental set for this ODE consists of a pair linearly independent solutions y1, 42. But there are times when only one function, call it y1, is available and we would like to find a s linearly independent solution. We can find 2 using the method of reduction of order. First, under the necessary assumption the a2 (x) #0 we rewrite the equation as a1 (x) a2(z) ao(x) q(x) = a2(x) y" +p(x)y +q(x)y = 0 p(x) Then the method of reduction of order gives a second linearly independent solution as e-Sp(z)dz - da f(エ) Y2(x) = Cyiu = Cy1(x) where C is an arbitrary constant. We can choose the arbitrary constant to be anything we like. One useful choice is to choose C so that all the constants in front reduce to 1. For example, if we c Y2 = C3e2 then we can choose C = 1/3 so that y2 = e2. Given the problem r?y" + 6xy' – 36y = 0 and a solution y1 = 1* Applying the reduction of order method to this problem we obtain the following y7(x) = p(r) = and e- SP(z)dz So we have e-Sp(z)dz dx = = xp Finally, after making a selection of a value for C as described above (you have to choose some nonzero numerical value) we arrive at Y2(x) = Cy,u = So the general solution to 9y" – 6y' + 4y = 0 can be written as y = C1y1 + C2Y2 = C1 +c2
Giveň á šéčónd órder linéär hómögenéðuš différêntial équatión a2(x)y" +a1(x)y' + ao(x)y=0 we know that a fundamental set for this ODE consists of a pair linearly independent solutions y1, 42. But there are times when only one function, call it y1, is available and we would like to find a s linearly independent solution. We can find 2 using the method of reduction of order. First, under the necessary assumption the a2 (x) #0 we rewrite the equation as a1 (x) a2(z) ao(x) q(x) = a2(x) y" +p(x)y +q(x)y = 0 p(x) Then the method of reduction of order gives a second linearly independent solution as e-Sp(z)dz - da f(エ) Y2(x) = Cyiu = Cy1(x) where C is an arbitrary constant. We can choose the arbitrary constant to be anything we like. One useful choice is to choose C so that all the constants in front reduce to 1. For example, if we c Y2 = C3e2 then we can choose C = 1/3 so that y2 = e2. Given the problem r?y" + 6xy' – 36y = 0 and a solution y1 = 1* Applying the reduction of order method to this problem we obtain the following y7(x) = p(r) = and e- SP(z)dz So we have e-Sp(z)dz dx = = xp Finally, after making a selection of a value for C as described above (you have to choose some nonzero numerical value) we arrive at Y2(x) = Cy,u = So the general solution to 9y" – 6y' + 4y = 0 can be written as y = C1y1 + C2Y2 = C1 +c2
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
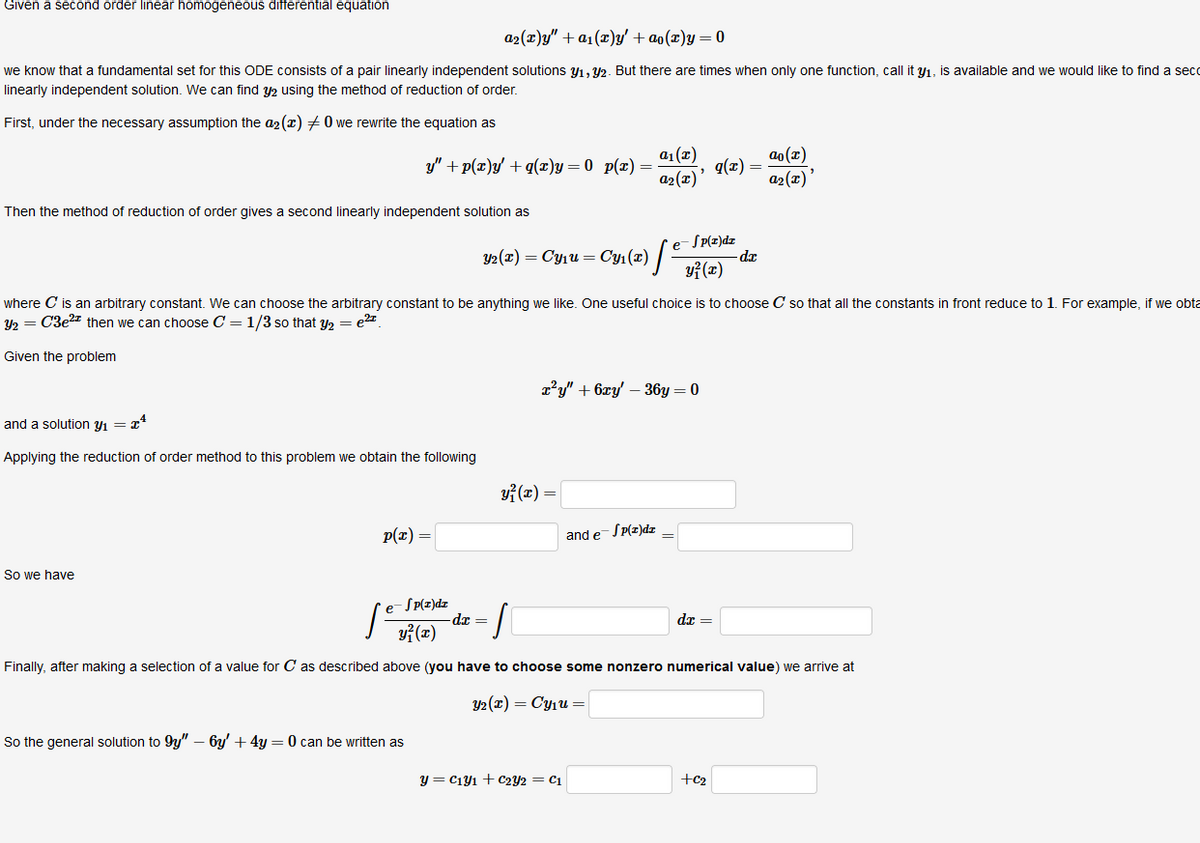
Transcribed Image Text:Given a second order linear homogeneous differential equation
a2(r)y" +a1(x)y' + ao(x)y=0
we know that a fundamental set for this ODE consists of a pair linearly independent solutions y1, 2. But there are times when only one function, call it y1, is available and we would like to find a seco
linearly independent solution. We can find y2 using the method of reduction of order.
First, under the necessary assumption the a2(r) 7 0 we rewrite the equation as
a1(r)
q(x)
a2(x)
ao (x)
y" +p(x)y' +q(x)y = 0 p(x) =
a2(x)'
Then the method of reduction of order gives a second linearly independent solution as
e-Sp(z)dz
- dr
yf (x)
32 (2) — Суи — Сул (г) | -
where C is an arbitrary constant. We can choose the arbitrary constant to be anything we like. One useful choice is to choose C so that all the constants in front reduce to 1. For example, if we obta
Y2 = C3e2 then we can choose C = 1/3 so that y2 = e2.
Given the problem
z'y" + 6xy' – 36y = 0
and a solution y1 = x*
Applying the reduction of order method to this problem we obtain the following
yf (x) =
p(x) =
S p(z)dz
and e
So we have
- S p(z)dz
dr =
e
dx =
Finally, after making a selection of a value for C as described above (you have to choose some nonzero numerical value) we arrive at
Y2 (x) = Cyu =
So the general solution to 9y" – 6y' + 4y = 0 can be written as
y = C1y1 + C2Y2 = C1
+c2
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 5 steps with 29 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning