Have you ever wondered how your calculator can produce a numeric approximation for complicated numbers like e, or In(2)? After all, the only operations a calculator can really perform are addition, subtraction, multiplication, and division, the operations that make up polynomials. This activity provides the first steps in understanding how this process works. Throughout the activity, let f(z)=e*. Part (a) The tangent line to feat z=0 is L(z) = The formula L(z) can be used to appriximate e since L(1) f(1) = e. In particular, L(1) =
Have you ever wondered how your calculator can produce a numeric approximation for complicated numbers like e, or In(2)? After all, the only operations a calculator can really perform are addition, subtraction, multiplication, and division, the operations that make up polynomials. This activity provides the first steps in understanding how this process works. Throughout the activity, let f(z)=e*. Part (a) The tangent line to feat z=0 is L(z) = The formula L(z) can be used to appriximate e since L(1) f(1) = e. In particular, L(1) =
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter4: Polynomial And Rational Functions
Section4.3: Zeros Of Polynomials
Problem 67E
Related questions
Question
q12 and q13
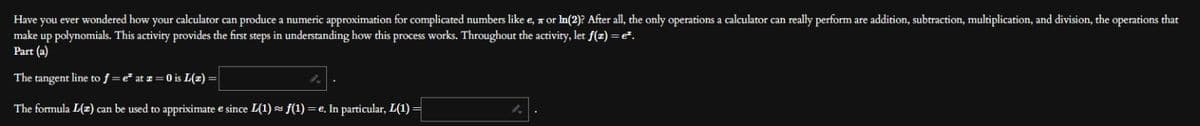
Transcribed Image Text:Have you ever wondered how your calculator can produce a numeric approximation for complicated numbers like e, or ln(2)? After all, the only operations a calculator can really perform are addition, subtraction, multiplication, and division, the operations that
make up polynomials. This activity provides the first steps in understanding how this process works. Throughout the activity, let f(z) = e².
Part (a)
The tangent line to f = e² at z = 0 is L(z)
The formula L(z) can be used to appriximate e since L(1) ≈ f(1) = e. In particular, L(1) =
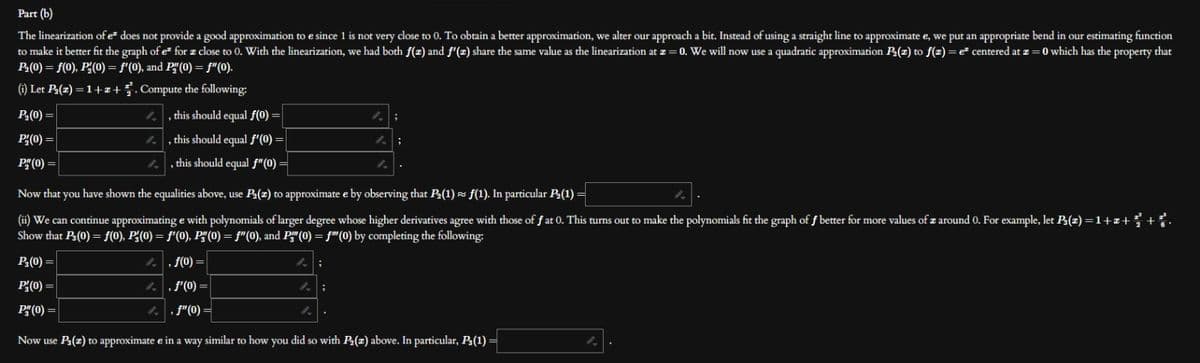
Transcribed Image Text:Part (b)
The linearization of e* does not provide a good approximation to e since 1 is not very close to 0. To obtain a better approximation, we alter our approach a bit. Instead of using a straight line to approximate e, we put an appropriate bend in our estimating function
to make it better fit the graph of e² for z close to 0. With the linearization, we had both f(z) and f'(z) share the same value as the linearization at z = 0. We will now use a quadratic approximation P₂(z) to f(z) = e centered at z=0 which has the property that
P₂(0) = f(0), P₂(0) = f'(0), and P(0) = f"(0).
(i) Let P₂(z)=1+z+. Compute the following:
1.
P₂(0) =
P'(0) =
P" (0)
this should equal f(0) =
this should equal f'(0) =
, this should equal f"(0):
1.
1.
1.
1.
;
Now that you have shown the equalities above, use P₂(z) to approximate e by observing that P₂(1) ≈ f(1). In particular P₂(1) =
(ii) We can continue approximating e with polynomials of larger degree whose higher derivatives agree with those of f at 0. This turns out to make the polynomials fit the graph of f better for more values of z around 0. For example, let P3(z)=1+2+2 +3.
Show that P3(0) = f(0), P'(0) = f'(0), P″(0) = ƒ"(0), and P!" (0) = f" (0) by completing the following:
P3(0) =
P'(0) =
4, f(0) =
&, f'(0) =
f" (0)
P" (0) =
Now use P3(z) to approximate e in a way similar to how you did so with P₂(z) above. In particular, P3(1)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images

Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage