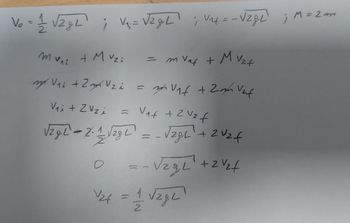Homework Help is Here – Start Your Trial Now!
Science
Advanced Physics
Consider a pendulum of mass m and length L. The suspension point of the pendulum it’s on a height L. The pendulum is released from the horizontal position, on its lowest point collides with a block of mass M=2m, the block has a velocity of -V0 in the x axis. The pendulum bounces reaching the initial, horizontal position. If the collision is elastic, A) Find de speed v0 as a function of m, L and g. B) Find de velocity of the block M after the collision.

Consider a pendulum of mass m and length L. The suspension point of the pendulum it’s on a height L. The pendulum is released from the horizontal position, on its lowest point collides with a block of mass M=2m, the block has a velocity of -V0 in the x axis. The pendulum bounces reaching the initial, horizontal position. If the collision is elastic, A) Find de speed v0 as a function of m, L and g. B) Find de velocity of the block M after the collision.

icon
Related questions
Question

Hi, con you help me with this problem please?

Consider a pendulum of mass m and length L. The suspension point of the pendulum it’s on a height L. The pendulum is released from the horizontal position, on its lowest point collides with a block of mass M=2m, the block has a velocity of -V0 in the x axis. The pendulum bounces reaching the initial, horizontal position. If the collision is elastic,

A) Find de speed v0 as a function of m, L and g.

B) Find de velocity of the block M after the collision.

 

Thanks.

m L Vo M X
Transcribed Image Text:m L Vo M X
Expert Solution
steps

Step by step

Solved in 3 steps

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

in step 3, is there a minus ( - ) missing in the initial velocity of the block?

Solution
Bartleby Expert
SEE SOLUTION
Follow-up Question

Knowing that v0= 1/2 sqrt (2gL) ; v1i = sqrt(2gL) ; v1f = -sqrt(2gL) ; M=2m

By the conservation of the momentum, wouldn't the velocity of the block after the collision be v0?

Thanks

Vo = 1/2 VZgZ ; Vq;= VzgL1 ; Vn<= -√zgL;M=2m gL muni + M v zi = m Vnf + M vzt na Vai +23 Vzi = 36V₁f +235 Vzf V₁ i + 2 V zi = V₁+ + 2 v₂ f √zgl-2.1/₂ √zgL¹ = -√zg[+2Vzf O -VzgL¹+2Vzf V24 = 1/2 √2g2² Vzgl 2
Transcribed Image Text:Vo = 1/2 VZgZ ; Vq;= VzgL1 ; Vn<= -√zgL;M=2m gL muni + M v zi = m Vnf + M vzt na Vai +23 Vzi = 36V₁f +235 Vzf V₁ i + 2 V zi = V₁+ + 2 v₂ f √zgl-2.1/₂ √zgL¹ = -√zg[+2Vzf O -VzgL¹+2Vzf V24 = 1/2 √2g2² Vzgl 2
Solution
Bartleby Expert
SEE SOLUTION