Inflation, nominal interest rates, and real rates. Given the following information, . estimate the real rate with the approximate nominal interest rate equation and the true nominal interest rate equation (Fisher effect) for each set of nominal and inflation rates. First, fill in the approximate real interest rate in the following table: (Round to two decimal places.)
Inflation, nominal interest rates, and real rates. Given the following information, . estimate the real rate with the approximate nominal interest rate equation and the true nominal interest rate equation (Fisher effect) for each set of nominal and inflation rates. First, fill in the approximate real interest rate in the following table: (Round to two decimal places.)
Chapter7: Types And Costs Of Financial Capital
Section: Chapter Questions
Problem 2EP
Related questions
Question
Please see attached
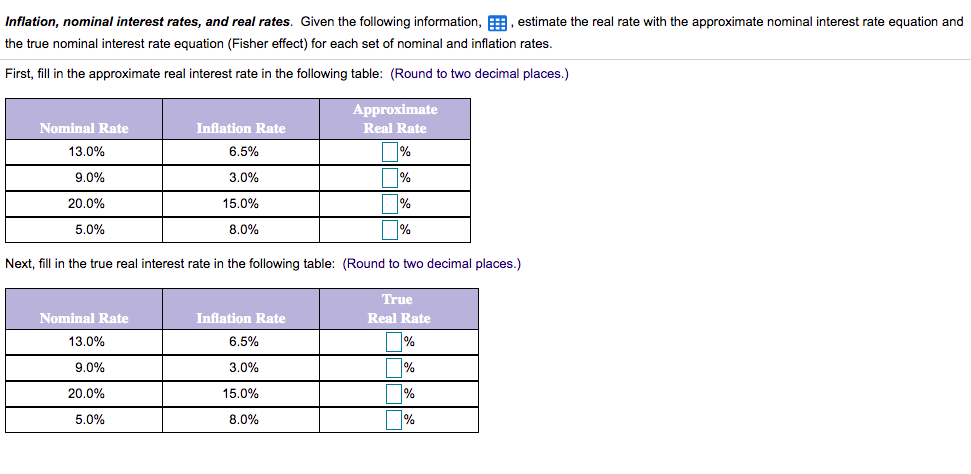
Transcribed Image Text:Inflation, nominal interest rates, and real rates. Given the following information, E, estimate the real rate with the approximate nominal interest rate equation and
the true nominal interest rate equation (Fisher effect) for each set of nominal and inflation rates.
First, fill in the approximate real interest rate in the following table: (Round to two decimal places.)
Approximate
Nominal Rate
Inflation Rate
Real Rate
13.0%
6.5%
%
9.0%
3.0%
%
20.0%
15.0%
%
5.0%
8.0%
%
Next, fill in the true real interest rate in the following table: (Round to two decimal places.)
True
Nominal Rate
Inflation Rate
Real Rate
13.0%
6.5%
7%
9.0%
3.0%
%
%
%
20.0%
15.0%
5.0%
8.0%
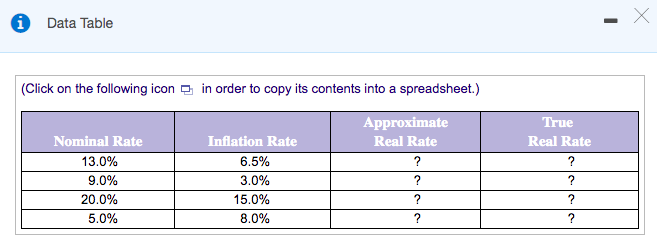
Transcribed Image Text:i Data Table
(Click on the following icon a in order to copy its contents into a spreadsheet.)
Approximate
True
Nominal Rate
Inflation Rate
Real Rate
Real Rate
13.0%
6.5%
?
9.0%
3.0%
?
?
20.0%
15.0%
5.0%
8.0%
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 6 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, finance and related others by exploring similar questions and additional content below.Recommended textbooks for you



Pfin (with Mindtap, 1 Term Printed Access Card) (…
Finance
ISBN:
9780357033609
Author:
Randall Billingsley, Lawrence J. Gitman, Michael D. Joehnk
Publisher:
Cengage Learning



Pfin (with Mindtap, 1 Term Printed Access Card) (…
Finance
ISBN:
9780357033609
Author:
Randall Billingsley, Lawrence J. Gitman, Michael D. Joehnk
Publisher:
Cengage Learning