Juestion 2 Proot Given a line segment, constructing a midpoint with Euclid propositions. We will show that we can find the midpoint of a line segment using straightedge and compass. In Euclid geometry, we know that a Midpoint is a point in the exact middle of a given straight line segment. We will be proving this using Proposition 1 that is To construct an equilateral triangle on a given finite straight line. We will also be referring to Proposition 9 to bisect a given rectilinear angle. Putting these propositions together we will be able to construct a midpoint to any given segment.
Juestion 2 Proot Given a line segment, constructing a midpoint with Euclid propositions. We will show that we can find the midpoint of a line segment using straightedge and compass. In Euclid geometry, we know that a Midpoint is a point in the exact middle of a given straight line segment. We will be proving this using Proposition 1 that is To construct an equilateral triangle on a given finite straight line. We will also be referring to Proposition 9 to bisect a given rectilinear angle. Putting these propositions together we will be able to construct a midpoint to any given segment.
Trigonometry (MindTap Course List)
8th Edition
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Charles P. McKeague, Mark D. Turner
Chapter1: The Six Trigonometric Functions
Section: Chapter Questions
Problem 2GP
Related questions
Question
use Venema 0.6.3 that in order to explain why CD is the perpendicular bisector of AB
in the picture capture explain what has to be prove

Transcribed Image Text:0.6.3. The perpendicular bisector of a segment AB is a line € such that l intersects AB
at its midpoint and l IAB. Prove the following theorem.
Pointwise Characterization of Perpendicular Bisector. A point P lies on the per-
pendicular bisector of AB if and only if PA = PB.
OP OQ
Proof : (forward direction) Suppose point P lies on
the perpendicular bisector of
Our goal is to show PA = PB.
Notice the triangles AAMP and ABMP
Congruent "by SAS with
included angles at M. Thus the
corresponding sides PA and PB are
congruent and PA = PB.
segment AB.
are
A
M
B
(backward direction) Given segment AB and
point P Such that PA= PB, we want to
show P is on the perpendicular bisector of
AB. Let M be the midpoint of AB.
Consider line PM. We Know it is a bisector
of AB and want to show the angles
Z AMP and BMP are right. The
triangles AAMP and ABMP are congruent
midpoint, PM is common,
by Šss (since M was
and PA = PB by hypothesis). Thus the
corresponding angles <AMP and <BMP are
congruent. But they also make a linear
pair,
So
can conclude both LAMP and <BMP
we
are right angles. So line PM is the perpendicular
bisector of AB (and paint P is on
Q.E.D.
Note: If P=M, then aso P is on the I bisector.
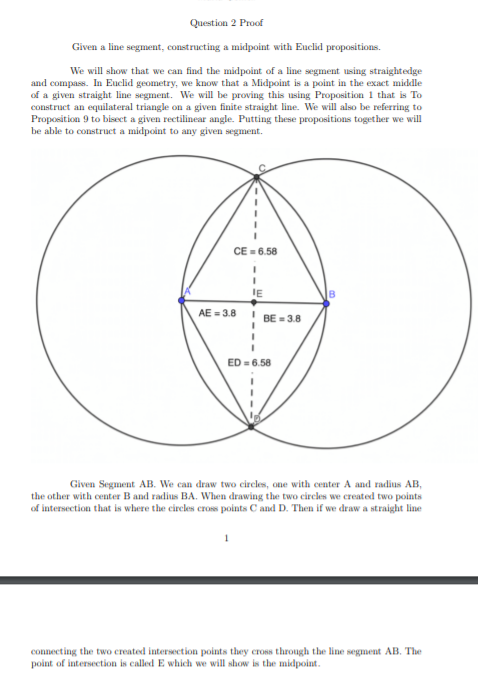
Transcribed Image Text:Question 2 Proof
Given a line segment, constructing a midpoint with Euclid propositions.
We will show that we can find the midpoint of a line segment using straightedge
and compass. In Euclid geometry, we know that a Midpoint is a point in the exact middle
of a given straight line segment. We will be proving this using Proposition 1 that is To
construct an equilateral triangle on a given finite straight line. We will also be referring to
Proposition 9 to bisect a given rectilinear angle. Putting these propositions together we will
be able to construct a midpoint to any given segment.
CE = 6.58
IE
AE = 3.8
BE = 3.8
ED = 6.58
Given Segment AB. We can draw two circles, one with center A and radius AB,
the other with center B and radius BA. When drawing the two circles we created two points
of intersection that is where the circles cross points C and D. Then if we draw a straight line
connecting the two created intersection points they cross through the line segment AB. The
point of intersection is called E which we will show is the midpoint.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage