Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
Let G be an abelian group. prove: H = {g € G||g| <∞o} is a subgroup of G. We need to prove that H ‡ Ø) and Vx, y ≤ H : xy¯¹ ɛ H. We know that e € H, because |e| = 1 < ∞, H‡Ø. Furthermore, if we take x, y = H, we know that xª = yb=1 for a, b = Z, so (xy−¹)ab = (xª)b(yb)−ª = 1, -1 › |xy¯¹| < ∞ and xy EH. G is not abelian, H doesn't have to be a subgroup. For example choose G = D∞, so H = {d€ Do | |d| <∞}. oth sr and sr² have order 2, but srsr² = r has infinite order, so r H. Therefore H is not a bgroup of G.

Let G be an abelian group. prove: H = {g € G||g| <∞o} is a subgroup of G. We need to prove that H ‡ Ø) and Vx, y ≤ H : xy¯¹ ɛ H. We know that e € H, because |e| = 1 < ∞, H‡Ø. Furthermore, if we take x, y = H, we know that xª = yb=1 for a, b = Z, so (xy−¹)ab = (xª)b(yb)−ª = 1, -1 › |xy¯¹| < ∞ and xy EH. G is not abelian, H doesn't have to be a subgroup. For example choose G = D∞, so H = {d€ Do | |d| <∞}. oth sr and sr² have order 2, but srsr² = r has infinite order, so r H. Therefore H is not a bgroup of G.

Elements Of Modern Algebra
Elements Of Modern Algebra
8th Edition
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Gilbert, Linda, Jimmie
Chapter3: Groups
Section3.4: Cyclic Groups
Problem 41E: Let G be an abelian group. Prove that the set of all elements of finite order in G forms a subgroup...
See similar textbooks
icon
Related questions
Question

I have the following question and solution, the assignment is to give feedback about the solution and the way its written.

Let G be an abelian group. To prove: H = {g €G ||g| <∞} is a subgroup of G. We need to prove that H ‡ Ø and Vx, y ≤H : xy-¹ € H. We know that e € H, because |e| = 1 < ∞, so H ‡ Ø). Furthermore, if we take x, y € H, we know that xª = y³ = 1 for a, b = Z, so -a (xy-¹)ab = (xª)b(y³)¯ = 1, so xy-¹ <∞ and xy-¹ € H. If G is not abelian, H doesn't have to be a subgroup. For example choose G = D∞, so H = {de D∞ | |d| <∞}. Both sr and sr² have order 2, but srsr² = r has infinite order, so r H. Therefore H is not a subgroup of G.
Transcribed Image Text:Let G be an abelian group. To prove: H = {g €G ||g| <∞} is a subgroup of G. We need to prove that H ‡ Ø and Vx, y ≤H : xy-¹ € H. We know that e € H, because |e| = 1 < ∞, so H ‡ Ø). Furthermore, if we take x, y € H, we know that xª = y³ = 1 for a, b = Z, so -a (xy-¹)ab = (xª)b(y³)¯ = 1, so xy-¹ <∞ and xy-¹ € H. If G is not abelian, H doesn't have to be a subgroup. For example choose G = D∞, so H = {de D∞ | |d| <∞}. Both sr and sr² have order 2, but srsr² = r has infinite order, so r H. Therefore H is not a subgroup of G.
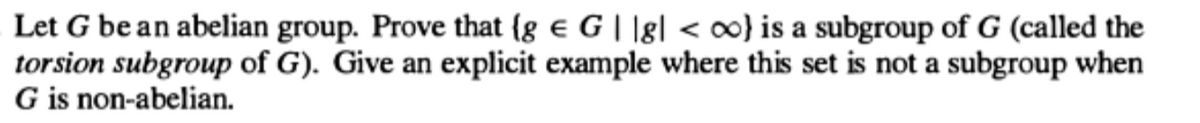
Let G be an abelian group. Prove that {g G||g| < oo}) is a subgroup of G (called the torsion subgroup of G). Give an explicit example where this set is not a subgroup when G is non-abelian.
Transcribed Image Text:Let G be an abelian group. Prove that {g G||g| < oo}) is a subgroup of G (called the torsion subgroup of G). Give an explicit example where this set is not a subgroup when G is non-abelian.
Expert Solution
steps

Step by step

Solved in 3 steps

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer