Let G (Z,+) and let n be a positive integer. Let H nZ = {na : a E Z}. We know that H is a subgroup of G. Describe the right cosets of H and G and find |G H.
Q: SUCH THAT LET H BE A PROPER SUBGROUP OF G V x,y € G-H, xy EH. PROVE THAT HAG.
A:
Q: Let G=U(18) and H={1,17} be a subgroup of G. The number of distinct left cosets of H in G is: * O 3…
A: Number of left/right coset of H in G = index of H in G
Q: Let G=U(18) and H={1,7,13} be a subgroup of G. The number of distinct left cosets of H in G is: * 4.
A:
Q: The set of all even integers 2Z is a subgroup of (Z, +) Then the right coset -3 + 2Z contains the…
A: Given that 2Z is the set of all even integers.
Q: by LetG = {(ª : a, b, , c, d e Z under addition let H EG : a +b + c + d = 1 € Z} H is a %3D subgroup…
A:
Q: et H ≤ S4 be the subgroup consisting of all permutations σ that satisfy σ(1) = 1. Find at least 4…
A: This is a good exercise in working with cosets. We first find out the subgroup $H$ and then working…
Q: Let G=U(20) and H={1,9} be a subgroup of G. The number of distinct left cosets of H in G is: * 4 O 5…
A: The solution is given as
Q: Let G=U(18) and H={1,17} be a subgroup of G. The number of distinct left cosets of H in G is: * O 5…
A: .
Q: Let G=U(20) and H={1,9} be a subgroup of G. The number of distinct left cosets of H in G is: 5.
A: Third option is correct. Answer is 4.
Q: Let G=U(18) and H={1,17} be a subgroup of G. The number of distinct left cosets of H in G is: * O 4…
A: Given: G=U(18) H={1,17} is a subgroup of G. Note:The number of distinct left cosets of H in G is…
Q: Let n > 2 be an integer, and let X C Sn × S, be the set X = {(ơ, T) | 0(1) = T(1)}. Show that X is…
A:
Q: Let H be a subgroup of G. If a and b are elements of G such that aH = bH, then Ja| = |b|. %3D
A: Given that Let H be a subgroup of G. If a and b are elements of G such that aH = bH, then a=b. To…
Q: The set of all even integers 2Z is a subgroup of (Z, +) Then the right coset -5 + 2Z contains the…
A:
Q: Let G=U(18) and H={1,7,13} be a subgroup of G. The number of distinct left cosets of H in G is: * O…
A: The solution is given as
Q: empity subsel Hef a Ha,bE H. G. Pawe that the intersection Hhk is also a subaroup. Eseercise I (a)…
A:
Q: 10. Let (G, *) be a group, and let H≤ G. Define N(H) = {x € G: x¹ *H* x = H} [Normalizer of H in G].…
A:
Q: Let H and K be subgroups of a group G. (a) Define HK = {hk | he H, ke K}. Show that if K is normal…
A: We will solve all the three parts. Given that H and K are subgroup of G
Q: Let H be a subgroup of G and let a, b E G. If aH = bH, then * На 1 — НЬ 1 О На %3Dнь На-1 %3D НЬ-1…
A: H is a subgroup of G and a,b belongs to G. If aH=bH then a and b lies in the same left coset of H.…
Q: The following is a subgroup of GL2(R) (which you do not need to prove): {[: '] {o aa, b, d e R, ad #…
A:
Q: b) LetG : a, b,.c,d € z under additlon, let H - {(" ) €G : a + b+c +d - 0 € Z} . Prove or disprove…
A:
Q: The set of all even integers 2Z is a subgroup of (Z, +) Then the right coset -3 + 2Z contains the…
A: Given: 2Z is a subgroup of (Z,+). We have to find the right coset of -3+2Z.
Q: Let G=U(18) and H={1,7,13} be a subgroup of G. The number of distinct left cosets of H in G is * 3 4…
A:
Q: Let G=U(20) and H={1,9} be a subgroup of G. The number of distinct left cosets of H in G is: *
A:
Q: The set of all even integers 2Z is a subgroup of (Z, +) Then the right coset -5 + 2Z contains the…
A: 2Z ={ ......... , -8, -6 , -4 , -2 , 0 , 2, 4, 6 , 8, ....}
Q: Let G and H be groups, and let 0 : G -» H be a {x E G 0(x) = e} is called the kernel of 0 and is…
A: From the given information:Let G and H be the groups
Q: 72 please
A:
Q: Let H be the subgroup {(1),(12)} of S3. Find the distinct right cosets H in S3,write out their…
A:
Q: Let G=U(18) and H={1,17} be a subgroup of G. The number of distinct left cosets of H in G is: * O 5…
A: By definition of Group of units, Let Un is the set of units in ℤn where n≥1. Then Un is a…
Q: Exercise 12, We identify S, with the sulgreup { 1,2,3} f Sy. Denode by v the four-subgroup (a) Prove…
A: We shall solve first three question only as per company guidelines. For others kindly post again by…
Q: What is the order of the cyclic subgroup of U5 generated by a = cos + i sin ? 108 degrees 3 10 3 10
A: Order Given: a=cos3π5+isin3π5 So, a2=cos3π5+isin3π52 ( Using De Moivre's theorem…
Q: 4. a) Let H be the set of elements [a b] of G of GL(2,R) such that ab- bc = 1. Show that H is a…
A:
Q: Let G=U(20) and H={1,9} be a subgroup of G. The number of distinct left cosets of H in G is: * O 4 O…
A: We have to solve given problem:
Q: Let G=U(18) and H={1,17} be subgroup of G. The number of distinct left cosets a of H in G is: * 3.
A: Given G=U(18) H ={1,17} We need to find the number of distinct left cosets of H in G
Q: Let G = (Z, +) and let n be a positive integer. Let H = nZ = {na : a € Z}. We know that H is a…
A:
Q: a b с d e f a b c d e f cdf a b e d e f a ecdb a b fc a b c d e f b f Answer: deca ecbfad Enter a…
A: We have to solve given problem:
Q: roblem 9.6 Let G = Z/100 and assume that H C G is a subgroup. xplain why it is impossible that |H|=…
A: Order of a subgroup divides the order of a group
Q: Let H and K be normal subgroups in G such that H n K = {1}. Show that hk = kh for all he H and k e…
A:
Q: Let G=U(18) and H={1,7,13} be a subgroup of G. The number of distinct left cosets of H in G is * O 5…
A:
Q: Let H be a subgroup of G. Show that if aH Deduce that H is normal in G if and only if every left…
A: Let's first show abH⊆Hab Let, abh=abh=ah1,b Since Hb=bHfor some h1∈H Therefore, abh=ah1b Since,…
Q: Let H < G. Recall that NG(H) = {g € G: gHg¯l = H}. 1). Prove that H 4 N(H). 2). If K is a subgroup…
A:
Q: Exercises: Is (H,*) a subgroup of (G,*) each of the following: (1) (Zs. +s), H={0, 6}. Find H. (2)…
A:
Q: b' e GL(2, IR) а Is Ga subgroup of GL(2, IR)? Let G
A: Note that, the general linear group is
Q: Q3) LetG = {( 5) : a, b.,c,d e z} under addition, %3D let H = {(" ) EG : +b+c+d = 1 € Z}. Prove or…
A: See the attachment
Q: Find all normal subgroups of G where(a) G = S3, (b) G = D4, the group of symmetries of the square,…
A: To find all the normal subgroups of the given (three) groups
Q: Let H be a subgroup of G. Show that if aH = Deduce that H is normal in G if and only if every left…
A: Given:- Let H be a subgroup of G. To prove:- If aH=Hb for some a,b ∈G then aH=Ha. also if H is…
Q: Let G=U(18) and H={1,17} be a subgroup of G. The number of distinct left cosets of H in G is: 3 O 5…
A:
Q: Let G=U(18) and H=(1,17} be a subgroup of G. The number of distinct left cosets of H in G is: * 3 O…
A:
Q: Let G = GL2(R). Prove that each of the following subsets is a subgroup of G. {[: a (а) Н a, b e R, a…
A:
Q: Let f : G → H be a homomorphism with kernel K. Show (a) K is a subgroup of G.(b) For any y ∈ H,…
A: Given:
Q: Let G=U(20) and H={1,9} be a subgroup of G. The number of distinct left cosets of H in G is: * 4
A: The solution is given as
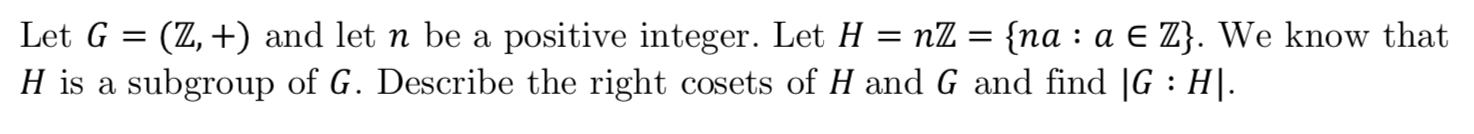
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 4 images

- Find the right regular representation of G as defined Exercise 11 for each of the following groups. a. G={ 1,i,1,i } from Example 1. b. The octic group D4={ e,,2,3,,,, }.16. Let be a subgroup of and assume that every left coset of in is equal to a right coset of in . Prove that is a normal subgroup of .Let be a subgroup of a group with . Prove that if and only if .
- 24. The center of a group is defined as Prove that is a normal subgroup of .With H and K as in Exercise 18, prove that K is a normal subgroup of HK. Exercise18: If H is a subgroup of G, and K is a normal subgroup of G, prove that HK=KH.18. If is a subgroup of the group such that for all left cosets and of in, prove that is normal in.
- 40. Find the commutator subgroup of each of the following groups. a. The quaternion group . b. The symmetric group .Let A be a given nonempty set. As noted in Example 2 of section 3.1, S(A) is a group with respect to mapping composition. For a fixed element a In A, let Ha denote the set of all fS(A) such that f(a)=a.Prove that Ha is a subgroup of S(A). From Example 2 of section 3.1: Set A is a one to one mapping from A onto A and S(A) denotes the set of all permutations on A. S(A) is closed with respect to binary operation of mapping composition. The identity mapping I(A) in S(A), fIA=f=IAf for all fS(A), and also that each fS(A) has an inverse in S(A). Thus we conclude that S(A) is a group with respect to composition of mapping.9. Find all homomorphic images of the octic group.
- For each of the following subgroups H of the addition groups Z18, find the distinct left cosets of H in Z18, partition Z18 into left cosets of H, and state the index [ Z18:H ] of H in Z18. H= [ 8 ] .27. Suppose is a normal subgroup of order of a group . Prove that is contained in , the center of .Let G be the group and H the subgroup given in each of the following exercises of Section 4.4. In each case, is H normal in G? Exercise 3 b. Exercise 4 c. Exercise 5 d. Exercise 6 e. Exercise 7 f. Exercise 8 Section 4.4 Let H be the subgroup e, of the octic group D4. Find the distinct left cosets of H in D4, write out their elements, partition D4 into left cosets of H, and give [D4:H]. Find the distinct right cosets of H in D4, write out their elements, and partition D4 into right cosets of H. Let H be the subgroup e, of the octic group D4. Find the distinct left cosets of H in D4, write out their elements, partition D4 into left cosets of H, and give [D4:H]. Find the distinct right cosets of H in D4, write out their elements, and partition D4 into right cosets of H. Let H be the subgroup e, of the octic group D4. Find the distinct left cosets of H in D4, write out their elements, partition D4 into left cosets of H, and give [D4:H]. Find the distinct right cosets of H in D4, write out their elements, and partition D4 into right cosets of H. Let H be the subgroup (1),(2,3) of S3. Find the distinct left cosets of H in S3, write out their elements, partition S3 into left cosets of H, and give [S3:H]. Find the distinct right cosets of H in S3, write out their elements, and partition S3 into right cosets of H. In Exercises 7 and 8, let G be the multiplicative group of permutation matrices I3,P3,P32,P1,P4,P2 in Example 6 of Section 3.5 Let H be the subgroup of G given by H=I3,P4={ (100010001),(001010100) }. Find the distinct left cosets of H in G, write out their elements, partition G into left cosets of H, and give [G:H]. Find the distinct right cosets of H in G, write out their elements, and partition G into right cosets of H. Let H be the subgroup of G given by H=I3,P3,P32={ (100010001),(010001100),(001100010) }. Find the distinct left cosets of H in G, write out their elements, partition G into left cosets of H, and give [G:H]. Find the distinct right cosets of H in G, write out their elements, and partition G into right cosets of H.

