Let Pn be the vector space of all polynomials of degree n or less in the variable æ. Let D² : P4 → P2 be the linear transformation that takes a polynomial to its second derivative. That is, D²(p(x)) = p" (x) for any polynomial p(æ) of degree 4 or less. A basis for the kernel of D² is { }. Enter a polynomial or a comma separated list of polynomials.
Let Pn be the vector space of all polynomials of degree n or less in the variable æ. Let D² : P4 → P2 be the linear transformation that takes a polynomial to its second derivative. That is, D²(p(x)) = p" (x) for any polynomial p(æ) of degree 4 or less. A basis for the kernel of D² is { }. Enter a polynomial or a comma separated list of polynomials.
Linear Algebra: A Modern Introduction
4th Edition
ISBN:9781285463247
Author:David Poole
Publisher:David Poole
Chapter6: Vector Spaces
Section6.2: Linear Independence, Basis, And Dimension
Problem 44EQ
Related questions
Question
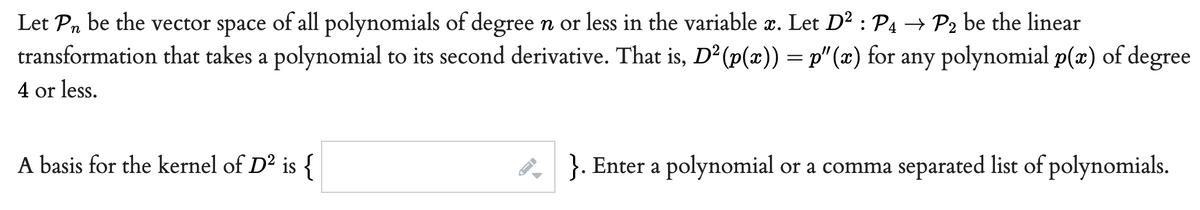
Transcribed Image Text:Let Pn be the vector space of all polynomials of degree n or less in the variable æ. Let D² : P4 → P2 be the linear
transformation that takes a polynomial to its second derivative. That is, D² (p(x)) = p" (x) for any polynomial p(x) of degree
4 or less.
A basis for the kernel of D² is {
8, }. Enter a polynomial or a comma separated list of polynomials.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning