Let p(t) = f be non-zero constant polynomial, let g(t) = dt+e be a linear polynomial (d‡0), and let r(t) = at² + bt+c be a quadratic polynomial (a + 0). Let's show that {p(t), g(t), r(t)} is a basis for P2. Since P₂ is isomorphic to R³ via the coordinate mapping (with respect to the standard basis for P₂), we can convert this into a question about vectors in IR³. In coordinates, the vectors p, q, r are respectively. To determine whether these vectors are linearly independent, we can cook up a matrix A with the above vectors as its columns and then determine whether A is invertible. Indeed, this matrix is invertible because its determinant is det (A) = and this is quantity is nonzero since a, d, f are all assumed to be nonzero. The determinant was easy to compute because the matrix above is choose one
Let p(t) = f be non-zero constant polynomial, let g(t) = dt+e be a linear polynomial (d‡0), and let r(t) = at² + bt+c be a quadratic polynomial (a + 0). Let's show that {p(t), g(t), r(t)} is a basis for P2. Since P₂ is isomorphic to R³ via the coordinate mapping (with respect to the standard basis for P₂), we can convert this into a question about vectors in IR³. In coordinates, the vectors p, q, r are respectively. To determine whether these vectors are linearly independent, we can cook up a matrix A with the above vectors as its columns and then determine whether A is invertible. Indeed, this matrix is invertible because its determinant is det (A) = and this is quantity is nonzero since a, d, f are all assumed to be nonzero. The determinant was easy to compute because the matrix above is choose one
Linear Algebra: A Modern Introduction
4th Edition
ISBN:9781285463247
Author:David Poole
Publisher:David Poole
Chapter6: Vector Spaces
Section6.4: Linear Transformations
Problem 3EQ: In Exercises 1-12, determine whether T is a linear transformation. T:MnnMnn defines by T(A)=AB,...
Related questions
Question
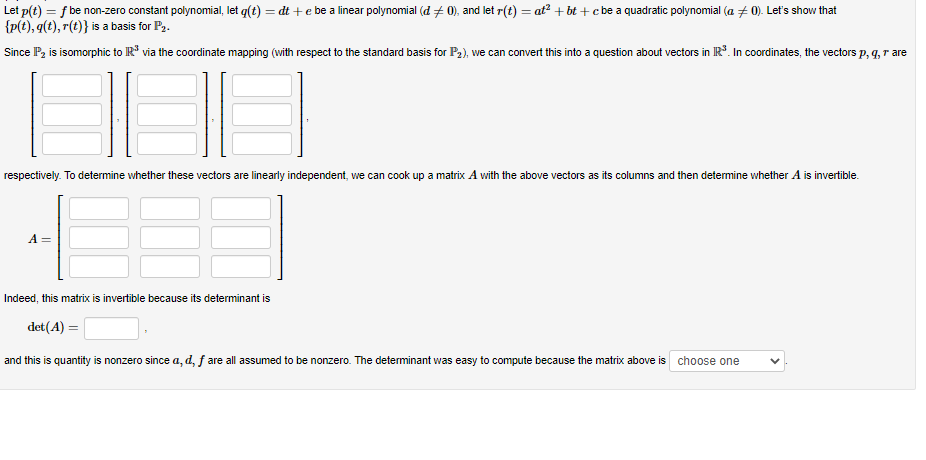
Transcribed Image Text:Let p(t) = f be non-zero constant polynomial, let g(t) = dt+e be a linear polynomial (d‡0), and let r(t) = at² + bt+c be a quadratic polynomial (a 0). Let's show that
{p(t), q(t), r(t)} is a basis for P₂.
Since P₂ is isomorphic to R³ via the coordinate mapping (with respect to the standard basis for P₂), we can convert this into a question about vectors in IR³. In coordinates, the vectors p, q, r are
respectively. To determine whether these vectors are linearly independent, we can cook up a matrix A with the above vectors as its columns and then determine whether A is invertible.
A =
Indeed, this matrix is invertible because its determinant is
det (A) =
and this is quantity is nonzero since a, d, f are all assumed to be nonzero. The determinant was easy to compute because the matrix above is choose one
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps

Recommended textbooks for you

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning