Homework Help is Here – Start Your Trial Now!
Math
Algebra
Let V be an inner product space. For a fixed vector v, in V, define T: V- R by T(v) = (v, v). Prove that Tis a linear transformation. Let v, be a vector in inner product space V, and define T: V-R by T(v) = (v, v). Now suppose v and w are vectors in V. By the properties of the inner product, we have the following. T(v + w) = (-Select-- v ---Select--- v = (v, --Select- v) + -Select-- v Select--- = T(v) + T(w) Next, supposec is a scalar. By the properties of the inner product, we have the following. T(cv) = Select-- v -Select-v) = c ---Select-- v ---Select-- = CT(v) Therefore, T: V-Ris a linear transformation.

Let V be an inner product space. For a fixed vector v, in V, define T: V- R by T(v) = (v, v). Prove that Tis a linear transformation. Let v, be a vector in inner product space V, and define T: V-R by T(v) = (v, v). Now suppose v and w are vectors in V. By the properties of the inner product, we have the following. T(v + w) = (-Select-- v ---Select--- v = (v, --Select- v) + -Select-- v Select--- = T(v) + T(w) Next, supposec is a scalar. By the properties of the inner product, we have the following. T(cv) = Select-- v -Select-v) = c ---Select-- v ---Select-- = CT(v) Therefore, T: V-Ris a linear transformation.

Linear Algebra: A Modern Introduction
Linear Algebra: A Modern Introduction
4th Edition
ISBN:9781285463247
Author:David Poole
Publisher:David Poole
Chapter6: Vector Spaces
Section6.4: Linear Transformations
Problem 34EQ
See similar textbooks
icon
Related questions
Question
Let V be an inner product space. For a fixed vector v, in V, define T: V→ R by T(v) = (v, v). Prove that Tis a linear transformation. be a vector in inner product space V, and define T: V →R by T(v) = (v, v). Now suppose v and w are vectors in V. By the properties of the inner product, we have the following. Let vo T(v + w) = ---Select--- v ---Select--- ♥ = (v, ---Select-- -Select--- v --Select-- v) = T(v) + T(w) Next, suppose c is a scalar. By the properties of the inner product, we have the following. T(cv) = --Select--- v ---Select--- v) = c ---Select--- ---Select--- v) = cT(v) Therefore, T: V- Ris a linear transformation.
Transcribed Image Text:Let V be an inner product space. For a fixed vector v, in V, define T: V→ R by T(v) = (v, v). Prove that Tis a linear transformation. be a vector in inner product space V, and define T: V →R by T(v) = (v, v). Now suppose v and w are vectors in V. By the properties of the inner product, we have the following. Let vo T(v + w) = ---Select--- v ---Select--- ♥ = (v, ---Select-- -Select--- v --Select-- v) = T(v) + T(w) Next, suppose c is a scalar. By the properties of the inner product, we have the following. T(cv) = --Select--- v ---Select--- v) = c ---Select--- ---Select--- v) = cT(v) Therefore, T: V- Ris a linear transformation.
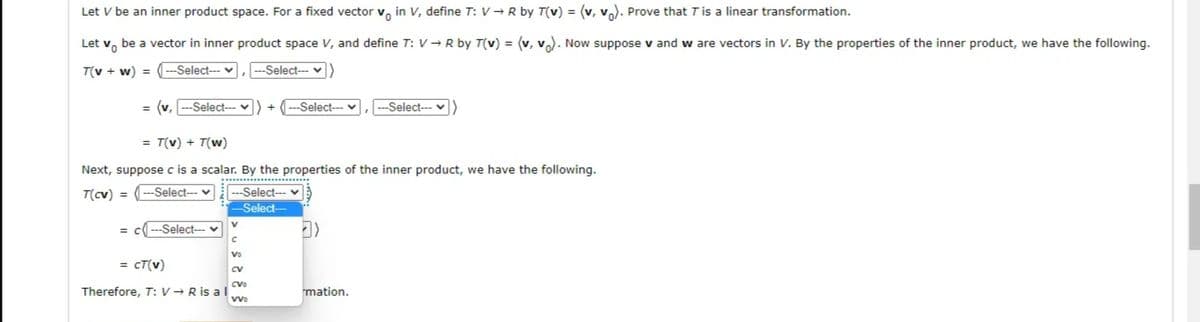
Let V be an inner product space. For a fixed vector v, in V, define T: V- R by T(v) = (v, v.). Prove that Tis a linear transformation. Let v, be a vector in inner product space V, and define T: V + R by T(v) = (v, v). Now suppose v and w are vectors in V. By the properties of the inner product, we have the following. T(v + w) = (---Select--- , --Select-- v) = (v, ---Select--- + (---Select- --Select--- v) = T(v) + T(w) Next, suppose c is a scalar. By the properties of the inner product, we have the following. ...... . T(cv) = -Select--- v ---Select- Select- = c ---Select-- v = cT(v) CV Cvo Therefore, T: V → R is a l mation.
Transcribed Image Text:Let V be an inner product space. For a fixed vector v, in V, define T: V- R by T(v) = (v, v.). Prove that Tis a linear transformation. Let v, be a vector in inner product space V, and define T: V + R by T(v) = (v, v). Now suppose v and w are vectors in V. By the properties of the inner product, we have the following. T(v + w) = (---Select--- , --Select-- v) = (v, ---Select--- + (---Select- --Select--- v) = T(v) + T(w) Next, suppose c is a scalar. By the properties of the inner product, we have the following. ...... . T(cv) = -Select--- v ---Select- Select- = c ---Select-- v = cT(v) CV Cvo Therefore, T: V → R is a l mation.
Expert Solution
steps

Step by step

Solved in 2 steps with 1 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer