Part 1 of 8 By re-ordering the sphere equation, we have z- 100 - - y, We can then parameterize this surface in rectangular coordinates as 2-V100 - 2 V100-- Part 2 of 8 Next, we need to find a restriction for u and v to describe only the part of the sphere that lies above the cone. We start by examining how the sphere and the cone intersect. Since both surfaces are symmetric around the z-axis, the sphere x++ - 100 intersects the cone z v in a circle. To find the equation of this cirele, we begin by substituting z V+y for z in the sphere equation, to get * y• ( y - 2., 2- 100. This can be further simplified to +- 50 P so Part 3 of8 The equation x+ y- 50 describes a cylinder, and the intersection circle is above the xy-plane and en this cylinder. The z-value of points on this circle can be found by solving z and x+- 50 simultaneously to find z, thereby obtaining z-V50 Part 4 of Since we want the portion of the sphere which is above this circle, we return to the parametric representation zV100-u - and limit z to be at least 50. We, therefore, have V 100-u - 2 vs0, which means u + s 5o. Part 5 of An alternative approach involves using spherical coordinates o, e, e), In spherical coordinates, the sphere has the equation p- 10 10 Part 6 of 8 Therefore, we can use and p as parameters and use the equations that allow us to convert from spherical to rectangular coordinates. We would then have *-10 sin cos e Subrmit Ske (you cancot.come back
Part 1 of 8 By re-ordering the sphere equation, we have z- 100 - - y, We can then parameterize this surface in rectangular coordinates as 2-V100 - 2 V100-- Part 2 of 8 Next, we need to find a restriction for u and v to describe only the part of the sphere that lies above the cone. We start by examining how the sphere and the cone intersect. Since both surfaces are symmetric around the z-axis, the sphere x++ - 100 intersects the cone z v in a circle. To find the equation of this cirele, we begin by substituting z V+y for z in the sphere equation, to get * y• ( y - 2., 2- 100. This can be further simplified to +- 50 P so Part 3 of8 The equation x+ y- 50 describes a cylinder, and the intersection circle is above the xy-plane and en this cylinder. The z-value of points on this circle can be found by solving z and x+- 50 simultaneously to find z, thereby obtaining z-V50 Part 4 of Since we want the portion of the sphere which is above this circle, we return to the parametric representation zV100-u - and limit z to be at least 50. We, therefore, have V 100-u - 2 vs0, which means u + s 5o. Part 5 of An alternative approach involves using spherical coordinates o, e, e), In spherical coordinates, the sphere has the equation p- 10 10 Part 6 of 8 Therefore, we can use and p as parameters and use the equations that allow us to convert from spherical to rectangular coordinates. We would then have *-10 sin cos e Subrmit Ske (you cancot.come back
Algebra and Trigonometry (MindTap Course List)
4th Edition
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:James Stewart, Lothar Redlin, Saleem Watson
Chapter12: Conic Sections
Section12.CR: Chapter Review
Problem 6CC
Related questions
Question
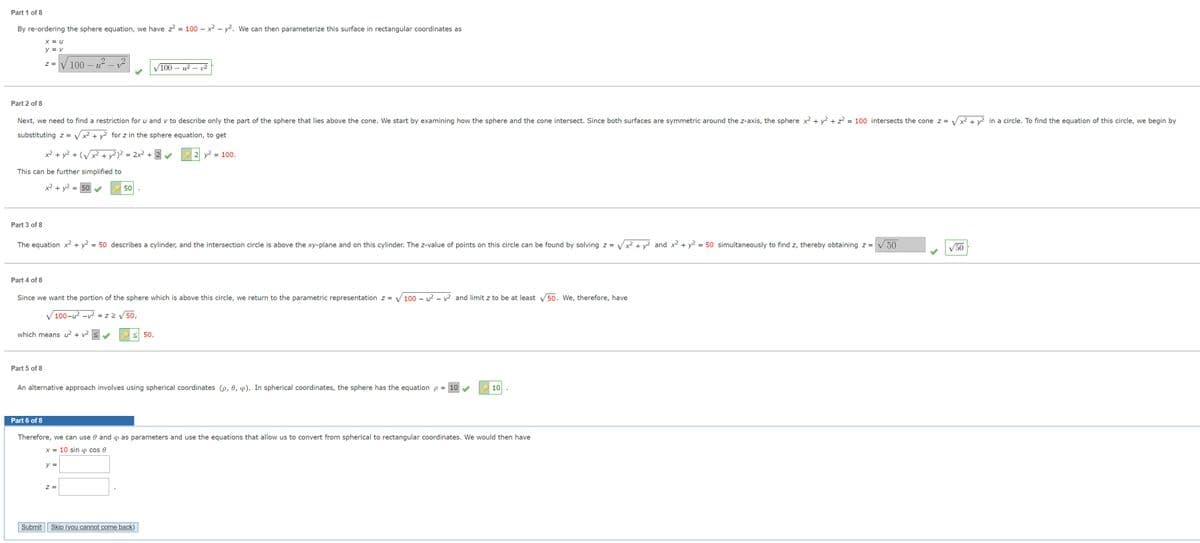
Transcribed Image Text:Part 1 of 8
By re-ordering the sphere equation, we have z? = 100 – x2 - y2. We can then parameterize this surface in rectangular coordinates as
X = u
y = v
V100 – u? – v²
Z =
100 – u?
v2
Part 2 of 8
Next, we need to find a restriction for u and v to describe only the part of the sphere that lies above the cone. We start by examining how the sphere and the cone intersect. Since both surfaces are symmetric around the z-axis, the sphere x2 + y2 + z?
= 100 intersects the cone z =
x² + y2 in a circle. To find the equation of this circle, we begin by
substituting z = V x2 + y? for z in the sphere equation, to get
x2 + y? + (Vx2 + y?)² = 2x² +
y?
= 100.
This can be further simplified to
x² + y2 =
= 50
50
Part 3 of 8
The equation x² + y2 = 50 describes a cylinder, and the intersection circle is above the xy-plane and on this cylinder. The z-value of points on this circle can be found by solving z =
Vx2 + y? and x2 + y2 = 50 simultaneously to find z, thereby obtaining z = 50
V50
Part 4 of 8
Since we want the portion of the sphere which is above this circle, we return to the parametric representation z =
100 – u? - v2 and limit z to be at least V50. We, therefore, have
V 100-u? -v2 = z > V50,
which means u2 + v2
50.
Part 5 of 8
An alternative approach involves using spherical coordinates (p, 0, 4). In spherical coordinates, the sphere has the equation p = 10
10
Part 6 of 8
Therefore, we can use e and o as parameters and use the equations that allow us to convert from spherical to rectangular coordinates. We would then have
X = 10 sin o cos e
y =
z =
Submit
Skip (you cannot come back)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images

Recommended textbooks for you

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,