Please implement the A* search algorithm in Python for the problem scenario below. Please explain your code and your approach.
PROBLEM SCENARIO
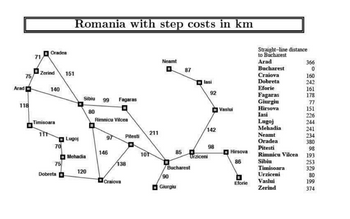
On holiday, a flight currently wants to travel to Bucharest from Arad. But there is
no direct way to Bucharest from Arad. However, the cities are connected with
each other like a graph. The distance between the connected cities are given. The
flight wants to travel through the most optimal way. To find the optimal path to
travel, another information is provided: the straight line distance between any city
and the final destination (Bucharest).
Now apply A* search to determine the most optimal value for the route Arad to
Bucharest and help the flight. You have to use the straight line distance as the
heuristic value for the cities.
City Heuristic value City Heuristic value
Arad 366 Mehadia 241
Bucharest 0 Neamt 234
Craiova 160 Oradea 380
Eforie 161 Pitesti 100
Fagaras 176 Rimnicu Vilcea 193
Dobreta 242 Timisoara 329
Hirsova 151 Urziceni 80
lasi 226 Vaslui 199
Lugoj 244 Zerind 374
For simplicity, assume these notations
Arad A Neamt F
Bucharest Z Oradea B
Craiova S Pitesti P
Eforie T Rimnicu Vilcea R
Fagaras O Timisoara C
Dobreta V Urziceni D
Hirsova N Vaslui H
lasi Q Zerind E
Lugoj G
Mehadia L
INPUTS
Your txt file should take each node followed by each destination it can reach and
their corresponding distance and heuristics. You are to read the file then ask the
user to input the starting and the destination point.
OUTPUTS
The output will contain the total distance from the starting point to the
destination followed by printing the nodes it followed to calculate the distance.
SAMPLE INPUT
In the text file:
Arad 366 Zerind 75 Sibiu 140 Timisoara 118
Zerind 374 Arad 75 Oradea 71
Oradea 380 Zerind 71 Sibiu 151
... ... ... ... ... ...
Bucharest 0 Pitesti 101 Fagaras 211 Giurgiu 90 Urziceni 85
Giurgiu 77 Bucharest 90
... ... ... ... ... …
The text file is arranged as follows:
Each line starts with a node followed by the heuristic of that node
Then the neighboring nodes and the distance from the parent node is given as a pair
All neighboring city-distance pairs are listed after the heuristic.
For example, the text file starts with Arad which has a heuristic of 366. It is the parent
node to Zerind, Sibiu and Timisoara which are 75, 140 and 118 km away from Arad.
Notice that since Bucharest is the End node which is why it has a heuristic of 0.
In console:
Start node: Arad
Destination: Bucharest
Sample output:
Path: Arad -> Sibiu -> Rimnicu -> Pitesti -> Bucharest
Total distance: 418 km
If there is no path found from the Start node to the End node, simply print “NO
PATH FOUND
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

- A bus driver has a job to show a group of tourists around different cities. All edges denote the pairs of cities connected by two-way roads. Each pair of neighboring cities on each edge has a bus service that runs between two cities. Each edge has a particular limit on the maximum number of passengers it can carry and the driver wants to take as many tourists as possible on each trip from departure city to the destination city. Note that the bus is big enough it can take any number of passengers as long as the roads permit. For the following road map of seven cities and the number on each edge indicates the passenger limit. For this specific example, the best route to take is 1 - 2 - 4 - 7 when 1 is the departure city and 7 is the destination city. Describe the pseudocode of your algorithm to find the best route (1-2-4-7 in our example) for any road graph to carry most tourists on a trip. Your description should be general, and not tied to a specific example. You must justify…arrow_forwardLet G = (V, E) be an undirected graph and each edge e ∈ E is associated with a positive weight ℓ(e).For simplicity we assume weights are distinct. Is the following statement true or false? Let P be the shortest path between two nodes s, t. Now, suppose we replace each edge weight ℓ(e) withℓ(e)^2, then P is still a shortest path between s and t.arrow_forwardThe clique problem is finding cliques in a diagram. A clique is a set of vertices that are adjacent to each other. The 4-clique is a set of four knots all connected. So, in this example of the 4-clique problem, we have a graph with 7 vertices. A brute force algorithm searched all possible combinations of four vertices and found a set that formed a clique. If you want to understand more about it, the problem (and if possible read on). Note that the clique problem is NP-complete, so deterministic search is not practical for large graph sizes. This makes it an ideal candidate for evolutionary exploration. In this problem, we have to assume that we are given the problem of implementing the 4-clique problem as an evolutionary algorithm for an arbitrary graph with an arbitrary number of vertices (an n-vertex graph). If 4 cliques are found, the algorithm succeeds. 1. Provide an algebraic expression, in terms of n, for the size of the phenotypic search space (the number of possible…arrow_forward
- The given inputs consist of two nodes (s, t) and a directed graph G = (V, E). In addition, each edge of the graph is either blue or red. The goal is to find a path from point s to point t such that red edges always follow blue edges. There need not be any red or blue borders on the route, but if there are, the red ones should follow the blue ones. Develop an algorithm that does the task in O(n + m) time and analyze its performance.arrow_forwardOne can manually count path lengths in a graph using adjacency matrices. Using the simple example below, produces the following adjacency matrix: A B A 1 1 B 1 0 This matrix means that given two vertices A and B in the graph above, there is a connection from A back to itself, and a two-way connection from A to B. To count the number of paths of length one, or direct connections in the graph, all one must do is count the number of 1s in the graph, three in this case, represented in letter notation as AA, AB, and BA. AA means that the connection starts and ends at A, AB means it starts at A and ends at B, and so on. However, counting the number of two-hop paths is a little more involved. The possibilities are AAA, ABA, and BAB, AAB, and BAA, making a total of five 2-hop paths. The 3-hop paths starting from A would be AAAA, AAAB, AABA, ABAA, and ABAB. Starting from B, the 3-hop paths are BAAA, BAAB, and BABA. Altogether, that would be eight 3-hop paths within this graph. Write a program…arrow_forwardConsider an undirected graph with n nodes and m edges. The goal is to find a path between two specified nodes u and v that maximizes the minimum weight of any edge along the path. Assume that all edge weights are positive and distinct. Design an algorithm to solve this problem with a time complexity of O(m log n).arrow_forward
- Consider eight points on the Cartesian two-dimensional x-y plane. a g C For each pair of vertices u and v, the weight of edge uv is the Euclidean (Pythagorean) distance between those two points. For example, dist(a, h) : V4? + 1? = /17 and dist(a, b) = v2? + 0² = 2. Because many pairs of points have identical distances (e.g. dist(h, c) V5), the above diagram has more than one minimum-weight spanning tree. dist(h, b) = dist(h, f) Determine the total number of minimum-weight spanning trees that exist in the above diagram. Clearly justify your answer.arrow_forward10. Apply Djikstra's Algorithm to find a shortest path from A to Z. Be sure to show each step of the algoriothm on a separate picture as discussed in class. Work carefully and pay attention to details. You need to clearly show how you are applying the algorithm. Also be sure to clearly name the verticies of a final shortest path Barrow_forwardGiven N cities represented as vertices V₁, V2, un on an undirected graph (i.e., each edge can be traversed in both directions). The graph is fully-connected where the edge eij connecting any two vertices vį and vj is the straight-line distance between these two cities. We want to search for the shortest path from v₁ (the source) to VN (the destination). ... Assume that all edges have different values, and €₁,7 has the largest value among the edges. That is, the source and destination have the largest straight-line distance. Compare the lists of explored vertices when we run the uniform-cost search and the A* search for this problem. Hint: The straight-line distance is the shortest path between any two cities. If you do not know how to start, try to run the algorithms by hand on some small cases first; but remember to make sure your graphs satisfy the conditions in the question.arrow_forward
- Write the PYTHON programming to solve with breadth-first search and build node-arcs with python code for the attached problem:arrow_forwardYou are organizing a programming competition, where contestants implement Dijkstra's algorithm. Given adirected graph G = (V, E) with integer-weight edges and a starting vertex s ∈ V , their programs are supposedto output triplets (v, v.d, v.π) for each vertex v ∈ V . Design an O(V +E) time algorithm that takes as inputthe original graph G in both adjacency matrix (G.M) and adjacency list (G.Adj) representations, startingvertex s, and the output of a contestant's program (given as an array A of triplets), and returns whetherA is the correct output for G. Write down the pseudocode for your algorithm, explain why it correctlyveri es the output, and analyze your algorithm's running time. You may assume that all edge weights of the input graph provided to the contestantsare nonnegative and A (the output of their programs) is in the valid format, i.e., you don't need to verifythat A is actually an array of triplets, with v and v.π being valid vertices and v.d being an integer.Can you…arrow_forwardThere are many applications of Shortest Path Algorithm. Consider the problem of solving a jumbled Rubik's Cube in the fewest number of moves. I claim that this problem can be solved using a Shortest Path Algorithm. Determine whether this statement is TRUE or FALSE. NOTE: if you want to check if this statement is TRUE, think about how the Rubik's Cube Problem can be represented as a graph. What are the vertices? Which pairs of vertices are connected with edges? What is your source vertex and what is your destination vertex? How would Dijkstra's Algorithm enable you to find the optimal sequence of moves to solve a jumbled cube in the fewest number of moves?arrow_forward