Prove that the two sets of conditions are equivalent. Here, Tis a linear transformation and u, v are two vectors and c, d are two scalars. Condition Set 1: T(cu + dv) = cT(u) + dT(v) Condition Set 2: T(u + v) = T(u) + T(v) T(cu) = cT(u) %3D %3D
Prove that the two sets of conditions are equivalent. Here, Tis a linear transformation and u, v are two vectors and c, d are two scalars. Condition Set 1: T(cu + dv) = cT(u) + dT(v) Condition Set 2: T(u + v) = T(u) + T(v) T(cu) = cT(u) %3D %3D
Elementary Linear Algebra (MindTap Course List)
8th Edition
ISBN:9781305658004
Author:Ron Larson
Publisher:Ron Larson
Chapter7: Eigenvalues And Eigenvectors
Section7.CM: Cumulative Review
Problem 3CM: Let T:RnRm be the linear transformation defined by T(v)=Av, where A=[30100302]. Find the dimensions...
Related questions
Question
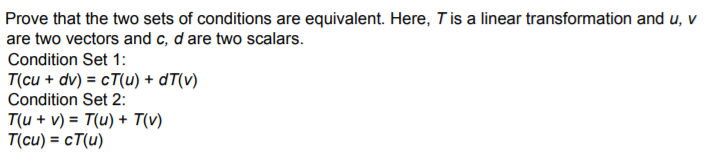
Transcribed Image Text:Prove that the two sets of conditions are equivalent. Here, Tis a linear transformation and u, v
are two vectors and c, d are two scalars.
Condition Set 1:
T(cu + dv) = cT(u) + dT(v)
Condition Set 2:
T(u + v) = T(u) + T(v)
T(cu) = cT(u)
%3D
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps

Recommended textbooks for you

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning