The solution to the recurrence T(n) = 4T(n/2) + n turns out to be T(n) = e(n). Show that a substitution proof with the assumption T(n) ≤ cn fails. Then show how to subtract a lower-order term to make a substitution proof work.

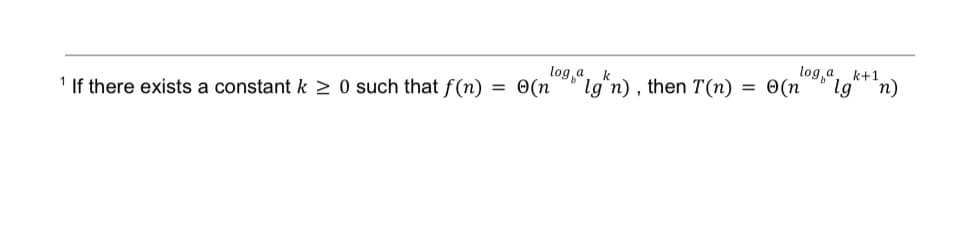
Required Proof:
Assuming T(n) < c*n^2 for some constant c, we can substitute it in the recurrence relation to get:
T(n) = 4T(n/2) + n < 4c(n/2)^2 + n = cn^2 + n
Since we want to prove that T(n) = O(n^2), we need to show that there exist constants c' and n0 such that T(n) <= c'n^2 for all n >= n0. However, we can see that this is not possible using the above inequality because cn^2 + n will always be greater than c'n^2 for any constant c' when n is sufficiently large. Therefore, the assumption that T(n) < c*n^2 fails to prove that T(n) = O(n^2).
To make a substitution proof work, we can subtract a lower-order term from T(n) before assuming T(n) < c*n^2. Let T'(n) = T(n) - an^b, where b > 2 and a is a constant to be determined later. Substituting T'(n) in the recurrence relation, we get:
T'(n) + an^b = 4[T'((n/2))] + n
= 4[(T(n/2) - a(n/2)^b)] + n
= 4T'(n/2) + 2an^b + n
Subtracting an additional an^b term from both sides, we get:
T'(n) = 4T'(n/2) + (n - an^b) <= 4c(n/2)^2 + (n - an^b) = cn^2 + (1 - 4a/4^(b-1))n^b
For the above inequality to hold, we need 1 - 4a/4^(b-1) to be negative, which implies that a > 4^(b-1)/4. Therefore, we can choose a = 1/4^(b-2) and get:
T'(n) <= cn^2 - n^(b-2)
Trending now
This is a popular solution!
Step by step
Solved in 2 steps


