Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
Suppose f: R → R is continuously differentiable. Show that if f'(x) > 0 for xo R, then there exists some interval I = (xo - 8, xo + 6) such that f|, : I → j bijective.

Suppose f: R → R is continuously differentiable. Show that if f'(x) > 0 for xo R, then there exists some interval I = (xo - 8, xo + 6) such that f|, : I → j bijective.

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question

This problem introduces a very reduced version of the inverse function theorem.

Suppose \( f : \mathbb{R} \to \mathbb{R} \) is continuously differentiable. Show that if \( f'(x_0) > 0 \) for some \( x_0 \in \mathbb{R} \), then there exists some interval \( I = (x_0 - \delta, x_0 + \delta) \) such that \( f|_I : I \to f(I) \) is bijective.
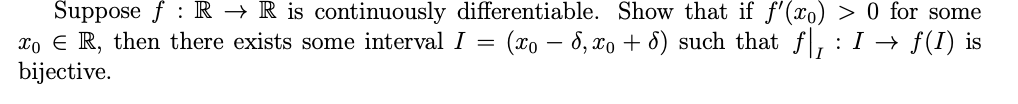
Transcribed Image Text:Suppose \( f : \mathbb{R} \to \mathbb{R} \) is continuously differentiable. Show that if \( f'(x_0) > 0 \) for some \( x_0 \in \mathbb{R} \), then there exists some interval \( I = (x_0 - \delta, x_0 + \delta) \) such that \( f|_I : I \to f(I) \) is bijective.
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS