Suppose that V(t) = (23)1.07 +5 sin(t) represents the value of a person's investment portfolio in thousands of dollars in year t, where t = 0 corresponds to January 1, 2020. Round each answer below to two places after the decimal. At what instantaneous rate is the portfolio's value changing on January 1, 2022? thousands of dollars per year Determine the value of V"(2). What do your answers above tell you about the way the portfolio's value is changing on January 1, 2022? the value of the portfolio is increasing, but its rate of increase is slowing down the value of the portfolio is increasing, and its rate of increase is speeding up the value of the portfolio is decreasing, and its rate of decrease is speeding up the value of the portfolio is decreasing, but its rate of decrease is slowing down
Suppose that V(t) = (23)1.07 +5 sin(t) represents the value of a person's investment portfolio in thousands of dollars in year t, where t = 0 corresponds to January 1, 2020. Round each answer below to two places after the decimal. At what instantaneous rate is the portfolio's value changing on January 1, 2022? thousands of dollars per year Determine the value of V"(2). What do your answers above tell you about the way the portfolio's value is changing on January 1, 2022? the value of the portfolio is increasing, but its rate of increase is slowing down the value of the portfolio is increasing, and its rate of increase is speeding up the value of the portfolio is decreasing, and its rate of decrease is speeding up the value of the portfolio is decreasing, but its rate of decrease is slowing down
Chapter6: Exponential And Logarithmic Functions
Section: Chapter Questions
Problem 29PT: A radiation safety officer is working with 112 grams of a radioactive substance. After 17 days,...
Related questions
Question

Transcribed Image Text:Suppose that V(t) = (23)1.07 +5 sin(t) represents the value of a person's investment portfolio in
thousands of dollars in year t, where t = 0 corresponds to January 1, 2020.
Round each answer below to two places after the decimal.
At what instantaneous rate is the portfolio's value changing on January 1, 2022?
thousands of dollars per year
Determine the value of V"(2).
What do your answers above tell you about the way the portfolio's value is changing on January 1, 2022?
the value of the portfolio is increasing, but its rate of increase is slowing down
the value of the portfolio is increasing, and its rate of increase is speeding up
the value of the portfolio is decreasing, and its rate of decrease is speeding up
the value of the portfolio is decreasing, but its rate of decrease is slowing down
Expert Solution
Step 1
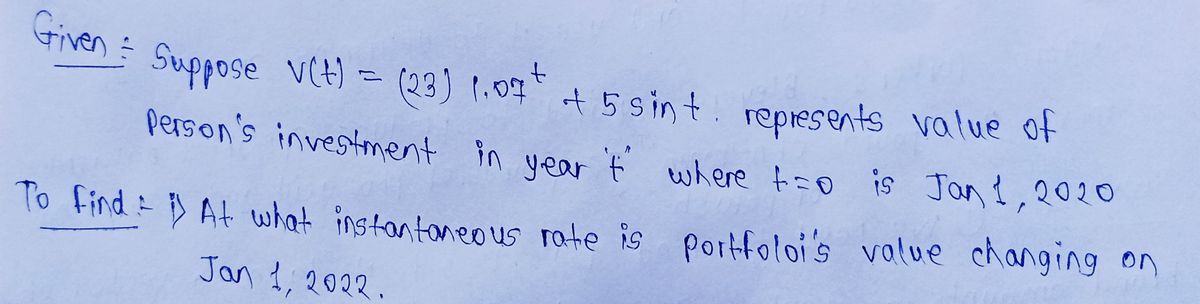
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage



Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
