The transformation of a function f(x) into a function g(x) is given by g(a) Af(BaH) K where the constants A vertically scales the function. (negative A reflects the function about the x-axis.) B horizontally scales the function. (negative B reflects the function about the y-axis.) H horizontally shifts the function. . K vertically shifts the function. Transform f() into g() where the transformation is g(z) f 1) The function f(x) is shown below in red. Graph the transformed function g(z) by first placing a dot at eac function and then click on the "line segment" button and connect the two blue dots. (Hint: Use pattern-matc constants A, B, H, and K.) 5- 2 6 -5 4 3 2 12 3 4 5 6 Clear All Draw·Dot LineSegment pe here to search Cortana Quick Key Windows 10 only PM F2 ovg F4 F6 10
The transformation of a function f(x) into a function g(x) is given by g(a) Af(BaH) K where the constants A vertically scales the function. (negative A reflects the function about the x-axis.) B horizontally scales the function. (negative B reflects the function about the y-axis.) H horizontally shifts the function. . K vertically shifts the function. Transform f() into g() where the transformation is g(z) f 1) The function f(x) is shown below in red. Graph the transformed function g(z) by first placing a dot at eac function and then click on the "line segment" button and connect the two blue dots. (Hint: Use pattern-matc constants A, B, H, and K.) 5- 2 6 -5 4 3 2 12 3 4 5 6 Clear All Draw·Dot LineSegment pe here to search Cortana Quick Key Windows 10 only PM F2 ovg F4 F6 10
Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)
6th Edition
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Bruce Crauder, Benny Evans, Alan Noell
Chapter5: A Survey Of Other Common Functions
Section5.6: Higher-degree Polynomials And Rational Functions
Problem 14E
Related questions
Question
Disregard the last bottom part. Please help with drawing the graph of what it’s asking in the top. Thanks.
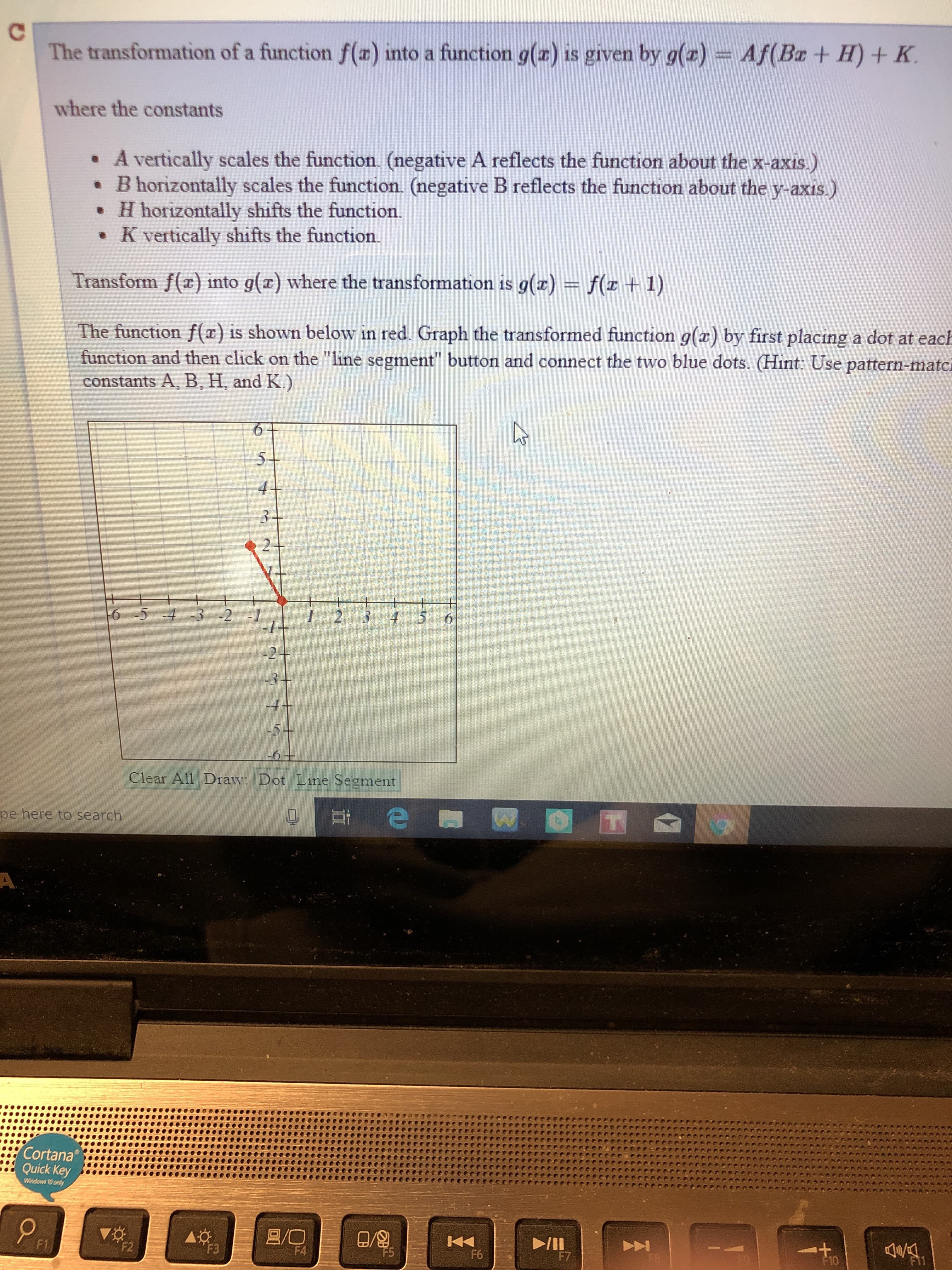
Transcribed Image Text:The transformation of a function f(x) into a function g(x) is given by g(a) Af(BaH)
K
where the constants
A vertically scales the function. (negative A reflects the function about the x-axis.)
B horizontally scales the function. (negative B reflects the function about the y-axis.)
H horizontally shifts the function.
. K vertically shifts the function.
Transform f() into g() where the transformation is g(z) f 1)
The function f(x) is shown below in red. Graph the transformed function g(z) by first placing a dot at eac
function and then click on the "line segment" button and connect the two blue dots. (Hint: Use pattern-matc
constants A, B, H, and K.)
5-
2
6 -5 4 3 2 12 3 4 5 6
Clear All Draw·Dot LineSegment
pe here to search
Cortana
Quick Key
Windows 10 only
PM
F2
ovg
F4
F6
10
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Recommended textbooks for you

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Big Ideas Math A Bridge To Success Algebra 1: Stu…
Algebra
ISBN:
9781680331141
Author:
HOUGHTON MIFFLIN HARCOURT
Publisher:
Houghton Mifflin Harcourt

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Big Ideas Math A Bridge To Success Algebra 1: Stu…
Algebra
ISBN:
9781680331141
Author:
HOUGHTON MIFFLIN HARCOURT
Publisher:
Houghton Mifflin Harcourt
